|
Question 907354: The inverse of the function y = x2 is still a function.
a) always
b) sometimes
c) never
Found 2 solutions by Fombitz, Theo:
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Never.
A function has one unique y value for each x value.
Since  gives one y value for two different x values (x and -x), the inverse would give two y values for a given x value and that violates the definition of a function.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! i think never.
y = plus or minus sqrt(x) is the inverse equation.
if x is positive, y will be a real number.
if x is negative, y will not be a real number.
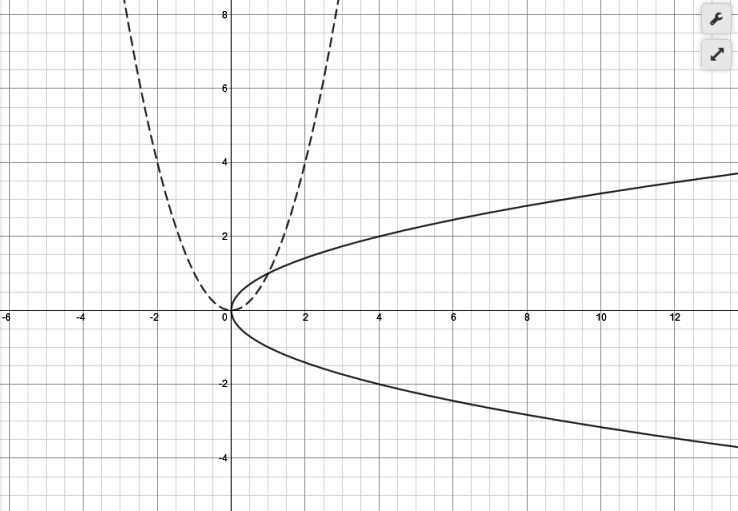
the graph of the equation is shown below:
the solids lines are the equation of y = plus or minus sqrt(x).
the dashed lines are the equation of y = x^2
the domain of y = x^2 is all real numbers and the range of y = x^2 is all real numbers greater than or equal to 0.
the domain of y = plus or minus sqrt(x) is all real numbers greater than or equal to 0 and the range of y = plus or minus sqrt(x) is all real numbers.
that is true of all inverse functions.
the domain of the original function is the range of the inverse function.
the range of the original function is the domain of the inverse function.
in this case, the inverse function is not a function, but a relation, because there are more than one value of y for any one value of x.
for it to be a function, every value of x must have one and only one value of y.
if any one value of x has more than one value of y, that's enough for it not to be a function, but to be a relation.
in this case, all values of x except for 0 have more than one value of y.
|
|
|
| |
