SOLUTION: Please need help with the following problems.Your help is appreciated. 1.The period of pendulum is directly proportional to the square root of its lenght.If the pendulum has a l

Algebra ->  Rational-functions -> SOLUTION: Please need help with the following problems.Your help is appreciated. 1.The period of pendulum is directly proportional to the square root of its lenght.If the pendulum has a l      Log On


   

Question 74739This question is from textbook algebra and trigonometry with analytic geometry
: Please need help with the following problems.Your help is appreciated.
1.The period of pendulum is directly proportional to the square root of its lenght.If the pendulum has a lenght of 6 feet and a period of 2 seconds,to what lenght should it be shortened to achieve a 1 second period?
2.Express the following statement as a formula with the value of the constant of propotionality determined with the given conditions;w varies directly as x and inversely as the square of y.If x=15 and y=5.then w=36.
3.find the roots of the polynomial x^3-x^2+16x-16.
4.Given that (3x-a)(x-2)(x-7)=3x^3-32x^2+81x-70,determine the value of a.
This question is from textbook algebra and trigonometry with analytic geometry

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
1.
Since the period is directly proportional to the square root of its length the equation looks like
T=k%2Asqrt%28L%29
So if L=6 and T=2, we can find k
2=k%2Asqrt%286%29
k=2%2Fsqrt%286%29
Now plug in T=1 to find L
1=%282%2Fsqrt%286%29%29%2Asqrt%28L%29
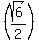
Multiply both sides by %28sqrt%286%29%2F2%29
%28sqrt%286%29%2F2%29%5E2=%28sqrt%28L%29%29%5E2Square both sides
6%2F4=L
L=4%2F3
So if the pendulum is 4/3 feet then the period is 1 second


2.
Since w varies directly as x, the equation looks like
w=kx
Since w also varies inversely as the square of y, it further looks like
w=kx%2Fy%5E2
If x=15, y=5 and w=36 then we can find k
36=k%2815%29%2F%285%29%5E2
36%2A25=k%28%2815%29%2Fcross%2825%29%29cross%2825%29Multiply both sides by 25
900%2F15=cross%2815%2F15%29kDivide both sides by 15
k=60
If we plugged in this value of k, the equation would look like:
w=60x%2Fy%5E2

3.
x%5E3-x%5E2%2B16x-16
x%28x%5E2-1%29%2B16%28x-1%29Factor out x from the first group and 16 from the 2nd
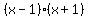
x%28x-1%29%28x%2B1%29%2B16%28x-1%29Factor x%5E2-1 to %28x-1%29%28x%2B1%29
%28x%28x%2B1%29%2B16%29%28x-1%29Add like terms of (x-1). Note: if we let y=x-1 we get x%28x%2B1%29y%2B16y=%28x%28x%2B1%29%2B16%29y
%28x%28x%2B1%29%2B16%29%28x-1%29=0Notice how we have a product of factors. Set them equal to zero.
x-1=0
x=1 There's one root
x%28x%2B1%29%2B16=0
x%5E2%2Bx%2B16=0Plug this into the quadratic formula to solve for x
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B1x%2B16+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%281%29%5E2-4%2A1%2A16=-63.

The discriminant -63 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -63 is + or - sqrt%28+63%29+=+7.93725393319377.

The solution is

Here's your graph:
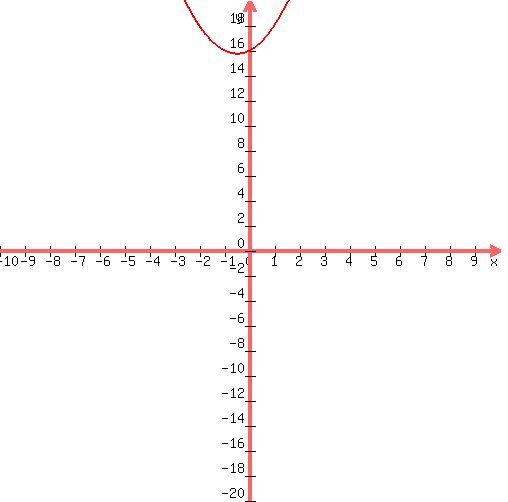graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B1%2Ax%2B16+%29

So the roots are:
x=1, x=-1%2F2%2B%281%2F2%29sqrt%2863%29i, and x=-1%2F2-%281%2F2%29sqrt%2863%29i





4.
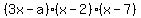%283x-a%29%28x-2%29%28x-7%29foil the first 2 parenthesis
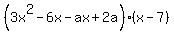%283x%5E2-6x-ax%2B2a%29%28x-7%29multiply the remaining 2 parenthesis
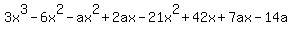
3x%5E3-6x%5E2-ax%5E2%2B2ax-21x%5E2%2B42x%2B7ax-14a
3x%5E3-6x%5E2-ax%5E2%2B2ax-21x%5E2%2B42x%2B7ax-14a=3x%5E3-32x%5E2%2B87x-70Set the equations equal to each other
Since the last term -14a=-70 so a=5
So the equation is
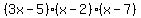
%283x-5%29%28x-2%29%28x-7%29
Note: I don't know if you copied the equation correctly or not but
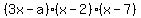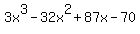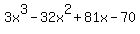%283x-a%29%28x-2%29%28x-7%29 is equal to 3x%5E3-32x%5E2%2B87x-70 not 3x%5E3-32x%5E2%2B81x-70 notice the change of 81 to 87 for the x coefficient.