SOLUTION: For questions 1–2, simplify the rational expression. State any restrictions on the variable help PLEASE? 1.) p^2-4p-32/p+4 2.) q^2+ 11q +24/ q^2 -5q -24

Algebra ->  Rational-functions -> SOLUTION: For questions 1–2, simplify the rational expression. State any restrictions on the variable help PLEASE? 1.) p^2-4p-32/p+4 2.) q^2+ 11q +24/ q^2 -5q -24       Log On


   

Question 711193: For questions 1–2, simplify the rational expression. State any restrictions on the variable
help PLEASE?
1.) p^2-4p-32/p+4

2.) q^2+ 11q +24/ q^2 -5q -24
Found 2 solutions by tutor_paul, dfvalen0223:
Answer by tutor_paul(519) About Me  (Show Source):
You can put this solution on YOUR website!
%28p%5E2-4p-32%29%2F%28p%2B4%29
---------------------
Restriction: p not equal to -4 (zero denominator is undefined)
Factor Numerator:
%28p-8%29%28p%2B4%29%2F%28p%2B4%29
Cancel out the (p+4) terms and you are left with:
highlight%28p-8%29
---------------------
%28q%5E2%2B11q%2B24%29%2F%28q%5E2-5q-24%29
---------------------
Factor Numerator:
%28q%2B3%29%28q%2B8%29%2F%28q%5E2-5q-24%29
Factor Denominator:
%28q%2B3%29%28q%2B8%29%2F%28q%2B3%29%28q-8%29
Note that q=-3 or q=8 give a zero denominator, so those values are not allowed
Cancel out the (q+3) terms and you are left with:
highlight%28%28q%2B8%29%2F%28q-8%29%29
======================
Good Luck,
tutor_paul@yahoo.com

Answer by dfvalen0223(2) About Me  (Show Source):
You can put this solution on YOUR website!
1). We can factorize the numerator:
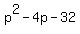
p%5E2-4p-32

then, we recognize the coefficients, the form of a quadratic equations is:
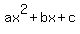
+ax%5E2%2Bbx%2Bc+
so:
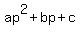
+ap%5E2%2Bbp%2Bc+
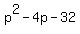
p%5E2-4p-32
+a=1+b=-4+c=-32
Now, we can use quadratic equations:
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ap%5E2%2Bbp%2Bc=0 (in our case 1p%5E2%2B-4p%2B-32+=+0) has the following solutons:

p%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-4%29%5E2-4%2A1%2A-32=144.

Discriminant d=144 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--4%2B-sqrt%28+144+%29%29%2F2%5Ca.

p%5B1%5D+=+%28-%28-4%29%2Bsqrt%28+144+%29%29%2F2%5C1+=+8
p%5B2%5D+=+%28-%28-4%29-sqrt%28+144+%29%29%2F2%5C1+=+-4

Quadratic expression 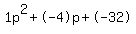1p%5E2%2B-4p%2B-32 can be factored:
1p%5E2%2B-4p%2B-32+=+1%28p-8%29%2A%28p--4%29
Again, the answer is: 8, -4. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-4%2Ax%2B-32+%29


roots are p=-4 and p = 8, so:
p%5E2-4p-32+=+%28p%2B4%29%28p-8%29
then:
+%28p%5E2-4p-32%29%2F%28p%2B4%29+=+%28p%2B4%29%28p-8%29%2F%28p%2B4%29+=+p-8
the restriction on this is: -4 because indetermine the expresion 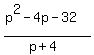%28p%5E2-4p-32%29%2F%28p%2B4%29 with zero in the denominator and this trend to infinite.
2) Again, We can factorize the numerator:
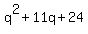
q%5E2%2B+11q+%2B24
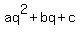
+aq%5E2%2Bbq%2Bc+
+a=1+b=11+c=24
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation aq%5E2%2Bbq%2Bc=0 (in our case 1q%5E2%2B11q%2B24+=+0) has the following solutons:

q%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2811%29%5E2-4%2A1%2A24=25.

Discriminant d=25 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-11%2B-sqrt%28+25+%29%29%2F2%5Ca.

q%5B1%5D+=+%28-%2811%29%2Bsqrt%28+25+%29%29%2F2%5C1+=+-3
q%5B2%5D+=+%28-%2811%29-sqrt%28+25+%29%29%2F2%5C1+=+-8

Quadratic expression 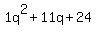1q%5E2%2B11q%2B24 can be factored:
1q%5E2%2B11q%2B24+=+1%28q--3%29%2A%28q--8%29
Again, the answer is: -3, -8. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B11%2Ax%2B24+%29

roots are q = -8 and q = -3, so:
q%5E2%2B+11q+%2B24+=+%28q%2B3%29%28q%2B8%29
too, We can factorize the denominator:
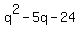
q%5E2+-5q+-24
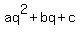
+aq%5E2%2Bbq%2Bc+
+a=1+b=-5+c=-24
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation aq%5E2%2Bbq%2Bc=0 (in our case 1q%5E2%2B-5q%2B-24+=+0) has the following solutons:

q%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-5%29%5E2-4%2A1%2A-24=121.

Discriminant d=121 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--5%2B-sqrt%28+121+%29%29%2F2%5Ca.

q%5B1%5D+=+%28-%28-5%29%2Bsqrt%28+121+%29%29%2F2%5C1+=+8
q%5B2%5D+=+%28-%28-5%29-sqrt%28+121+%29%29%2F2%5C1+=+-3

Quadratic expression 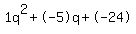1q%5E2%2B-5q%2B-24 can be factored:
1q%5E2%2B-5q%2B-24+=+1%28q-8%29%2A%28q--3%29
Again, the answer is: 8, -3. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-5%2Ax%2B-24+%29

roots are q = 8 and q = -3, so:
q%5E2%2B+11q+%2B24+=+%28q%2B3%29%28q-8%29
then:

the restriction on this is: 8 because indetermine the expresion %28q%2B8%29%2F%28q-8%29 with zero in the denominator and this trend to infinite.
Did you understand me?