SOLUTION: Find all horizontal and vertical asymptotes of the function. f(x)= X^2+2/ x^2-1

Algebra ->  Rational-functions -> SOLUTION: Find all horizontal and vertical asymptotes of the function. f(x)= X^2+2/ x^2-1      Log On


   

Question 631128: Find all horizontal and vertical asymptotes of the function.
f(x)= X^2+2/ x^2-1
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
I assume the equation is
f%28x%29=+%28x%5E2%2B2%29%2F%28x%5E2-1%29
If so, then please put multiple-term numerators and denominators in parentheses to make it clear.
Vertical asymptotes of a rational function, if any, occur for x values that make make the denominator zero. To find them, make the denominator zero and solve:
x%5E2-1+=+0
Solving:
%28x%2B1%29%28x-1%29+=+0
x+1 = 0 or x-1 = 0
x = -1 or x = 1
So we have two vertical asymptotes: x = -1 and x = 1

Horizontal asymptotes of a rational function, if any, occur for large positive and/or negative numbers. To find them, we have to figure out what happens when x is a large positive or negative number. Figuring this out is usually easier if you divide each term by the highest power of x that is present. With f(x) this would be x%5E2. Dividing each term by x%5E2:
f%28x%29=+%28x%5E2%2Fx%5E2%2B2%2Fx%5E2%29%2F%28x%5E2%2Fx%5E2-1%2Fx%5E2%29
which simplifies to:
f%28x%29=+%281%2B2%2Fx%5E2%29%2F%281-1%2Fx%5E2%29
Looking at this version of f(x) we can tell what happens to f(x) for large x's. When x gets to be large, positive or negative, 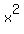in the denominator will have very large positive denominators. And what happens to fractions whose denominators get bigger and bigger? Answer: They get smaller and smaller, close to zero in fact. So as x gets to be very large, those two fractions becomes very close to zero. With this in mind we can figure out what happens to f(x) when x gets to be very large:
f(x) becomes very close to 1/1 (or just 1) because the two fractions are so close to zero they can be neglected. So our horizontal asymptote is:
y = 1.

P.S. Rules can be made for the horizontal asymptotes:
  • If the degree of the numerator is less than the degree of the denominator, then the horizontal asymptote is y = 0
  • If the degree of the numerator is equal to the degree of the denominator, then the horizontal asymptote is the ratio of the coefficients of those terms. This is what happened in your equation. The degree of the numerator and denominator are 2's because the highest exponent in both the numerator and denominator are 2's. And the coefficients of the two x%5E2 terms both happen to be 1's. This makes the horizontal asymptote the ratio of these two coefficients:
    y = 1/1 or just y = 1
  • If the degree of the numerator is greater than the degree of the denominator, then there will not be any horizontal asymptotes. (There may, however, be other types of asymptotes (slant, parabolic, etc.))