Question 583086: PLEASE help! My teacher didn't explain.
I have to write a rational function with the given asymptotes.
a. x=-2, y=0
b. x=4,y=0
c.x=2,x=1,y=1
d.x=0,y= -1
Thank you so much!
Found 2 solutions by KMST, solver91311:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) Vertical asymptotes. like x=-2, happen only when a denominator is zero.
 has a vertical asymptote at x=-2 has a vertical asymptote at x=-2
As x approaches -2, the denominator approaches zero and the absolute value of f(x) grows without bounds. The graph of  looks like this: looks like this:
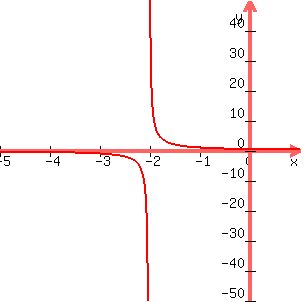 Coincidentally that function also has Coincidentally that function also has  as an asymptote, as you can see from the graph. as an asymptote, as you can see from the graph.
As the absolute value of x (and consequently of x+2) grows larger, and larger, f(x) grows closer and closer to zero. A  horizontal asymptote happens when your rational function is a quotient and the denominator polynomial has a higher degree than the numerator. horizontal asymptote happens when your rational function is a quotient and the denominator polynomial has a higher degree than the numerator.
CAUTION: Not every time a denominator is zero, you have a vertical asymptote.
If you make sure that the denominator, and only the denominator is zero at x=-2, you can be sure that the function will have an x=-2 asymptote.
If the numerator and denominator are zero at the same time, the function can be equivalent to another function that does not have a vertical asymptote.
For example,  is equivalent to is equivalent to  for all values of x except x=-2, and you know that for all values of x except x=-2, and you know that  graphs as a horizontal line with graphs as a horizontal line with  , and does not have a vertical asymptote. The graph for , and does not have a vertical asymptote. The graph for  looks just like the same horizontal y=1 line, except for a hole at x=-2, where p(x) does not exist. looks just like the same horizontal y=1 line, except for a hole at x=-2, where p(x) does not exist.
b) From what I said above, you must realize that for a vertical  asymptote, you need the denominator to be zero for asymptote, you need the denominator to be zero for  . .
 would work. It also has a would work. It also has a  asymptote, because the denominator, x-4 has degree 1, and the numerator, 1, has degree zero. asymptote, because the denominator, x-4 has degree 1, and the numerator, 1, has degree zero.
c)  has asymptotes has asymptotes  and and  because those are zeros of the denominator. because those are zeros of the denominator.
The only horizontal asymptote for  is is  and we need and we need  , but that is easy to fix: we just add 1. , but that is easy to fix: we just add 1.
 has has  , ,  and and  asymptotes. asymptotes.
You can make it look fancier:
 = = + +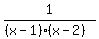 = = + +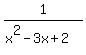 = =
d) For an  asymptote we want x as a factor in the denominator, but not tin the numerator. A asymptote we want x as a factor in the denominator, but not tin the numerator. A  asymptote would be easier, but you saw in part c) how you can get a horizontal asymptote at a different y value asymptote would be easier, but you saw in part c) how you can get a horizontal asymptote at a different y value
 = =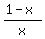 has has  and and  asymptotes. asymptotes.
 + +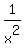 = =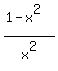 would work too. would work too.
Answer by solver91311(24713)   (Show Source): (Show Source):
|
|
|