|
Question 462539: I am really having a tough time with this question and would like some insight on how to solve it and what the answer is.
Find the numbers for which the rational expression is undefined.
s^3-8s/s^2-81
Thanks in advance!
Answer by math-vortex(648)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the numbers for which the rational expression is undefined.
s^3-8s/s^2-81
===================
There are two reasons that rational expressions are undefined in the real number system: (1) the square root of a negative number and (2) division by zero.
.
I want to make sure that I am solving the problem you intend for us to solve. Here is how what you typed would look in a textbook. I explain this one, and another related one further down:
.

.
In this case, we don't need to worry about the square root of a negative number because there are no square roots! We do need to look more closely at
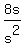
.
When we divide by s^2, we need to make sure we don't divide by zero. We ask ourselves, what values of s will make s^2=0. We see that when s=0, s^2=0.
.
We would say that

is undefined when s = 0.
.
.
--------------------
Here is the problem, I think you may have meant for us to solve:

.
We still don't need to worry about square roots, but we will need to examine
the denominator of this expression. We do not want the denominator to equal zero, because division by zero is undefined.
.
We ask ourselves which values of s make s^2-81=0. Let's work that out:

.
We notice that the left side of the equation is the difference of two squares, so we factor,

.
By the Zero Product Property,


or


.
We would say that

is undefined if s = 9 or s = -9.
.
hope this helps!
.
Ms.Figgy
math.in.the.vortex
|
|
|
| |