|
Question 390783: Make up a rational function graph that meets the following conditions:
a)it will have an oblique asymptote of slope "not equal" to 1.
b)it will have two x-intercepts, one of multiplicity 1 and the other 2.
c)it will have two vertical asymptotes.
Then, go through the complete process of graphing your rational function, showing all steps, including the long division.
Found 2 solutions by robertb, jsmallt9:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Whoa, STUDENT, you ask too much, he he. But I'll show you one rational function that will satisfy your conditions. Maybe some other tutor will show you the graphing/long dividing parts.
 . .
The degree of the top polynomial is 3, the bottom, 2, so after long division, the quotient is a linear function whose slope is 3/2. (You can even determine this by inspection!)
The roots of the function (which correspond to the x-intercepts) are 2 (multiplicity 1), and -1 (multiplicity 2).
The roots OF THE BOTTOM EXPRESSION, 1/2 and -3, yield the vertical asymptotes. The equations are exactly x = 1/2 and x = -3.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First we'll look at part b. The x-intercepts of a rational function will be where x makes the numerator zero. In order for an x-intercept to exist, (x-r) (where r is the intercept) must be a factor of the numerator. And for one x-intercept to be of multiplicity 2, (x-r) for that intercept must be a factor twice. So if  is the x-intercept of multiplicity 1 and is the x-intercept of multiplicity 1 and  is the intercept of multiplicity 2, then the numerator will have the following factors: is the intercept of multiplicity 2, then the numerator will have the following factors:
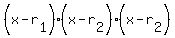 or or 
Next we'll look at part c. For a rational function to have two vertical asymptotes, there must be two numbers that make the denominator zero. If we call these two numbers  and and 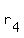 , then the denominator must have the factors: , then the denominator must have the factors:
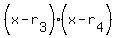
Last of all we will look at part a. So far our function looks like:

I hope it is easy to see that if we were to multiply out the numerator and denominator, the highest power term in the numerator would be  and the highest power term in the denominator would be and the highest power term in the denominator would be  . And if we divide . And if we divide  by by  we would get just "x". This would give us an oblique asymptote with a slope of 1 (since the coefficient of x is the slope). But we do not want a slope of 1. To get a different slope we need for the coefficients of the highest power terms to be different. One way to get different coefficients would be to add a constant factor to the numerator or denominator that is not a 1. If you add the factor to the numerator then that number will become the slope of the oblique asymptote. we would get just "x". This would give us an oblique asymptote with a slope of 1 (since the coefficient of x is the slope). But we do not want a slope of 1. To get a different slope we need for the coefficients of the highest power terms to be different. One way to get different coefficients would be to add a constant factor to the numerator or denominator that is not a 1. If you add the factor to the numerator then that number will become the slope of the oblique asymptote.
So our function now looks like:

All we need to do now is pick numbers for "a",  , ,  , ,  and and 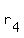 . In order to get the function you want, pick any number but 1 for "a" and make sure that . In order to get the function you want, pick any number but 1 for "a" and make sure that  , ,  , ,  and and 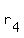 are all different numbers. As long as you follow the above rules your function will meet all the requirements of the problem no matter what numbers you pick! are all different numbers. As long as you follow the above rules your function will meet all the requirements of the problem no matter what numbers you pick!
As for the graphing, here are some key ideas:- The vertical asymptotes will be
 and and  . . - The graph will cross the x-axis at
 - The graph will have a relative maximum or minimum at the point (
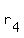 , 0). (If you do not know what a "relative maximum or minimum" means, then the graph will "bounce off" the x-axis at ( , 0). (If you do not know what a "relative maximum or minimum" means, then the graph will "bounce off" the x-axis at (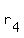 , 0)). (This happens because of the multiplicity of 2.) , 0)). (This happens because of the multiplicity of 2.) - If x=0 is not a vertical asymptote, then the graph will have a y-intercept. Put a zero in for x and figure out the value of the function when x is zero to determine the y-intercept.
- To find the equation of the oblique asymptote:
- Multiply out both the numerator and the denominator.
- Use long division to divide the numerator by the denominator.
- You should get something in the form of:
ax + b + expression/denominator
For large x values the expression/denominator fraction will approach zero. So the oblique asymptote will be the line:
y = ax + b
where "a" is the number you picked earlier and "b" is some other number (maybe even the same as "a") depending on how the division works out.
- Two x-intercepts, an oblique asymptote and possibly a y-intercept are not enough to figure out the whole graph. More points are needed. Pick some additional values for x and find the y value for each one. This will give you additional points. Keep finding additional points and plot them until you have a sense as to how the graph goes. Among the x values you try, I would suggest picking x values a little to the left and a little to the right of each of the two vertical asymptotes.
|
|
|
| |