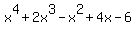
It's degree is 4, so it has four zeros. Now suppose the zeros were:
A, B, C, and D. Then it could be factored this way:
then if somebody were to take a long time with a large sheet of paper and
were to multiply that all the way, it would have sixteen terms before you
started combining terms. We are NOT going to do that, but only to ponder
the question what If somebody actually took the trouble to multiply those
four binomials all together. If they did the last term would have to be
ABCD. Therefore the product of all the zeros has to be -6.
Since the leading coefficient is 1, it factors as above and therefore
all feasible rational zeros are ± the factors of the absolute value of the
totally numerical term, the last term, which is -6 and its absolute value is +6.
The factors of 6 are these four integers: 1, 2, 3, and 6 itself. However
it is possible that their opposites, or negatives, could be
zeros also. So all the feasible zeros are these 8 possibilities:
+1, +2, +3, +6, -1, -2, -3 and -6
for which we usually just write:
±1, ±2, ±3, ±6
Let's find out if 1 is a zero. That is the same thing as trying to find out if
(x-1) is a factor of the polynomial. So we divide it by (x-1), but instead of
doing the long division like this:
_______________________
x - 1)x4 + 2x3 - x2 + 4x - 6
we do this synthetic division which is just a shortcut for getting the answer
to that long division.
1|1 2 -1 4 -6
| 1 3 2 6
1 3 2 6 0
Which means you have factored
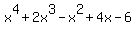as
Next we try to see if we can factor the 3rd degree
polynomial 
. It also ends with 6
so it has those same feasible zeros. So if 1 is a
zero, then (x-1) will be a factor so we divide
synthetically by x-1, and at the same time find out whether
1 is a zero:
1|1 3 2 6
| 1 4 6
1 4 6 12
No it isn't. So we have learned that 1 is not a zero and (x-1) is not
a factor of the polynomial.
So let's try to see if -1 is a zero, which is the same as seeing
if (x+1) is a factor of .
-1|1 3 2 6
| -1 -2 0
1 2 0 6
No it isn't. So we have learned that -1 is not a zero and (x+1) is not
a factor of the polynomial.
So let's try to see if -3 is a zero, which is the same as seeing
if (x+3) is a factor of .
-3|1 3 2 6
| -3 0 -6
1 0 2 6
Yes -3 is a zero. So we have learned that -3 is a zero and (x+3) is
a factor of the polynomial.
Which means we have so far factored
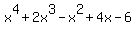first as
and now we have factored it further as
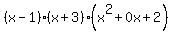or just
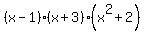The last thing to factor is 
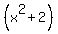When complex imaginary numbers are allowed we can factor the sum of
two perfect squares, even though we could not do this when
complex imaginary numbers were not allowed. To factor that we realize
that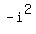 
just equals 1. So we can multiply the 2 by 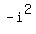without
changing the value.
To factor
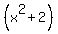multiply the 2 by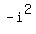
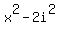Now we know that 
so we can
write the 2 as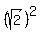 
, and we have:
Now it is the difference of two squares and we
know how to factor it.
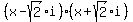So the complete factorization of
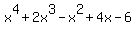is
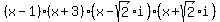and the four zeros are 1, -3, 
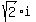and 
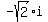Edwin
