5/y-3=y+7/2y-6+1
Hmmm! You didn't put parentheses to show where numerators
and denominators begin "(" and end ")", so I'm guessing you
mean one of two possibilities. I'll do both:
If you mean this:
Write the 
as 
so every term will
be a fraction:
Enclose each term in parentheses:
Factor the denominator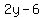 
as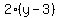 
Find the LCD, which is 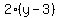, which we will
write as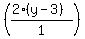 
and multiply each term
by it:
Cancel what will cancel:
All that's left is:
Distribute:
Combine like terms:
Add -1 to both sides
Divide both sides by 3:
Now we must check this answer, by
substituting it into the original, to make sure it
is not an extraneous solution:
But since division by 0 is undefined, there is
no solution. 3 was an extraneous, or "bogus"
solution, not an actual solution.
================
If you meant this:
Use 1 denominators so that all terms will be
fractions:
Enclose each term in parentheses:
Factor the denominator 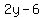as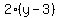
Find the LCD, which is 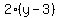, which we will
write as 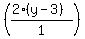and multiply each term
by it:
Cancel what will cancel:
All that's left is:
Distribute to remove parentheses:
Collect like terms:
Get 0 on the left by subtracting 10 from both sides:
or, since I like to have 0 on the right, not left,
I'll switch the sides:
That doesn't factor, so we use the quadratic
formula:
Factor 2 out of the numerator:
Cancel the 2 on top into the 4 on the bottom,
getting 2 on the bottom:
This is difficult to check. However if we were
to substitute that in the original, none of the
denominators would be 0, as they were in the
first way I assumed you meant. So these are both
solutions.
Edwin
