|
Question 161500: Hi, I was having problems with graphing and writing equations for graphs. The question asks "write and equation of for the following lines."
a) the line passing through (-7,6) and (42, 5).
b) the line perpendicular to y = 3+5x tht passes though the point (0,1)
Could you please help me figure out how to do this?
Thank you,
Ajeenah
Found 2 solutions by scott8148, gonzo:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) first, find the slope (m) __ slope=(change in y)/(change in x) __ m=(5-6)/(42-(-7)) __ m=-1/49
next, use point-slope to write the equation __ y-6=(-1/49)(x-(-7)) __ y-6=(-1/49)x-(1/7) __ y=(-1/49)x+(41/7)
b) perpendicular means that the slopes are negative reciprocals
__ the slope of the given line is 5, so the slope of the new line is -1/5
using point-slope (again) __ y-1=(-1/5)(x-0) __ y=(-1/5)x+1
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! -----
a) equation and graph for the line passing through (-7,6) and (42, 5).
-----
in order to graph this line you need a slope and a y intercept.
slope intercept form of the equation would be y = m*x + b where m is the slope and b is the y intercept.
you have 2 points, so you should be able to get the slope easy enough.
the equation for finding the slope is
m = ((y - y1) / (x - x1))
one of your points can be (x,y) and the other point can be (x1,y1)
let (x,y) = (-7,6)
let (x1,y1) = (42,5)
x - x1 becomes (-7) - (42) which becomes -49.
y - y1 becomes (6) - (5) which becomes 1.
m = -(1/49) = slope of the line.
-----
we substitute -1/49 for m in the slope intercept form of the equation to get
y = (-1/49)*x + b
-----
now we have to find b.
-----
you should be able to pick either of the two points to get b.
take the point (x1,y1) which is (42,5)
substitute 42 for x and 5 for y in the slope intercept form of the equation to get
y = (-1/49)*x + b to become
5 = (-1/49)*42 + b
which becomes
5 = -42/49 + b
add -42/49 to both sides of the equation and it becomes
5 + (42/49) = b
which becomes
5.857142857 = b
which is the same as
b = 5.857142857
-----
you now have the complete y intercept form of the equation which is
y = (-1/49)*x + 5.857142857
to prove this is correct, substitute values for (x,y) and for (x1,y1) in the equation.
----
substituting (-7,6) in the equation and it becomes
6 = (-1/49)*(-7) + 5.857142857
which becomes
6 = .142857143 + 5.857142857
which becomes
6 = 6
-----
substituting (42,5) in the equation and it becomes
5 = (-1/49)*(42) + 5.857142857
which becomes
5 = -.857142857 + 5.857142857
which becomes
5 = 5
-----
equation is good.
to graph it, you stay with the slope intercept form of the equation.
graph looks like this
scan below the graph to continue with the rest.
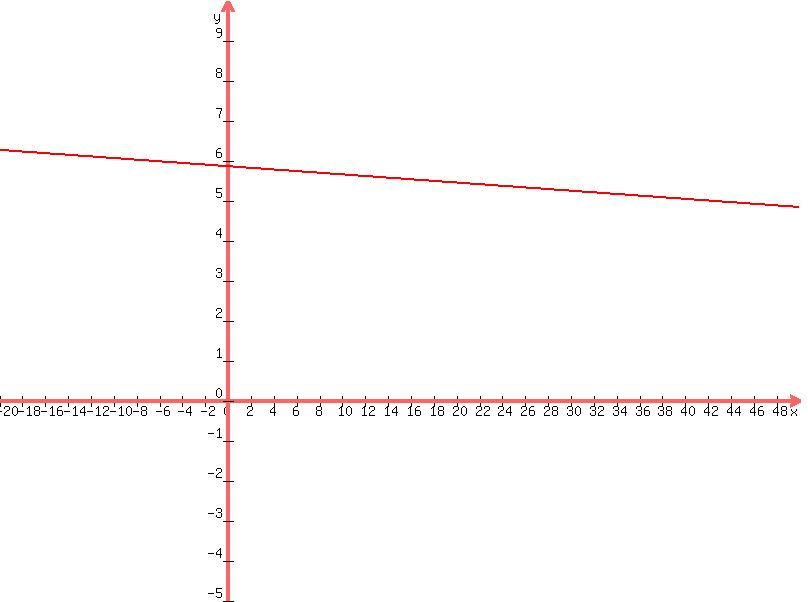
notice that when x = 0, y = 5.85714........
that's because the b in the slope intercept form of the equation is the value of y when x = 0.
you should be able to spot the point (45,5) and (-7,6) on the graph. look for x = +45 and scan up. look for x = -7 and scan up again. you won't be able to spot it exactly but you should be able to see that it's in the vicinity of where it should be.
-----
b) the line perpendicular to y = 3+5x that passes though the point (0,1)
-----
the line y = 3 + 5*x can be rewritten as
y = 5*x + 3
this puts it in the slope intercept form of the equation.
the slope intercept form of the equation is y = m*x + b where m is the slope and b is the y intercept when x = 0.
-----
if another line has the same slope as the original line, it will be parallel to the original line.
-----
if another line has a slope which is the negative reciprocal of the slope of the original line, then that line will be perpendicular to the original line.
-----
the original line is y = 5*x + 3.
this line has a slope of 5.
to get the negative reciprocal, we reverse the sign which makes it
-5
we then divide it by the square of itself.
-5 / (-5)*(-5) becomes 1/(-5).
the negative reciprocal of 5 is -(1/5).
-----
we now have the slope of the line perpendicular to the original line.
we need to find the y intercept.
the slope intercept form of the equation is y = m*x + b
since the slope is (-1/5) this equation becomes
y = (-1/5)*x + b
to solve for b, we substitute the point that it's passing through in the equation.
that point is (0,1) where the x value is 0 and the y value is 1.
substituting, the equation becomes
1 = (-1/5)*0 + b
which becomes
1 = 0 + b
which becomes
b = 1
-----
we now have the complete equation which is
y = (-1/5)*x + 1
to show you that it's perpendicular, i'll also show the original line on the graph so you can see them both.
the original line has the equation
y = 5*x + 3
the graph of that original equation will slope up going from left to the right.
the graph of the line perpendicular to it will slope down going from left to right at an angle that is not as steep as the angle of the original line going up.

|
|
|
| |