SOLUTION: Given y=9x^2-6x+3, What is the equation of the axis of symmetry? a)x=2/3 b)x=-1/3 c)x=-2/3 d)x=1/3 what are the coordinates of the vertex? Y-intercepts: X-intercepts:

You can put this solution on YOUR website!
Given , the x-coordinate of the vertex of the parabola is given by 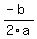, hence the axis of symmetry is . The y-coordinate of the vertex is the value of the function at the x-coordinate of the vertex. So the vertex is at (,)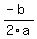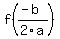

The x-intercepts are the values of x that make the function = 0, so set your function equal to 0 and solve the quadratic equation. If you end up with real roots, the x-intercepts are (x1,0) and (x2,0). If you end up with a conjugate pair of complex roots, then there are no x-intercepts.

The y-intercept is the value of the function at 0, so substitute 0 for x and do the arithmetic. The y intercept is (0,f(0))

And you are right, it does open up. A parabola opens upward whenever , and downward when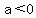