Question 135069: This is not a text book question
Given F(x) = 4x^2-1/x^2 -16
a) find x intercepts
b) y intercepts
c) Find the vertical asymptote (write as equation of a line)
d) Find the horizontal asymptote (write as equation of line)
e) For x>4, is there a value which F(x) cannot exceed, and/or value which F(x) cannot fall below? Explain
f) Find maximum or minimum in interval and state whether it is a maximum or minimum value for that interval
g) Describe what happens on graph when x approaches infinity.
I have several questions like this, but need direction on one, to help with the rest. I have the vertical asymptotes as 4 and -4 and the horizontal as 4.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
x-intercepts are where F(x)=0. Since we know that  if and only if if and only if  AND AND 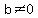 , all we need to to is set the numerator equal to zero, solve, and exclude any root that would make the denominator go to zero as well. The exclusion bit won't be a problem here, but you always need to consider the situation. , all we need to to is set the numerator equal to zero, solve, and exclude any root that would make the denominator go to zero as well. The exclusion bit won't be a problem here, but you always need to consider the situation.


 or or  . No exclusions required, so the intercepts are ( . No exclusions required, so the intercepts are ( , , ) and ( ) and ( , , ). ).
The y-intercept is at F(0), so evaluate  . Hence the y-intercept is ( . Hence the y-intercept is ( , , ) )
You have the right numbers for the asymptotes, but you are instructed to express them as equations, so you want  , ,  for the verticals, and for the verticals, and  for the horiziontal. for the horiziontal.
When  (or (or 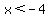 for that matter), F will always be a little more than 4. for that matter), F will always be a little more than 4. 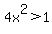 when when  , so the numerator is positive, and , so the numerator is positive, and 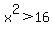 when when  , so the denominator is also positive. F(5) = 11 > 4 (you can calculate this out if you like) meaning that F > 4 when , so the denominator is also positive. F(5) = 11 > 4 (you can calculate this out if you like) meaning that F > 4 when  near near  and the constant terms will have less and less impact on the value of F as x gets larger. Further, x would have to be infinite in order for F to equal 4 if and the constant terms will have less and less impact on the value of F as x gets larger. Further, x would have to be infinite in order for F to equal 4 if  or or 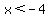 . That pretty much answers parts e and g. . That pretty much answers parts e and g.

Ignore the vertical (sort of) lines that intersect the x-axis at about -4 and 4. These are extraneous -- a shortcoming of the graph rendering system on this site.
Notice that the function has a local maximum on the interval (-4,4). Fortunately it happens to coincide with the y-intercept, i.e. the local maximum is at ( , , ). ).
If you actually need to prove that the local extrema is at ( , , ), you will have to take the first derivative of the function and set it equal to zero to find the point. Trying to render the quotient rule on this system is a horror, so I won't do it here. Write back if you want to see it. ), you will have to take the first derivative of the function and set it equal to zero to find the point. Trying to render the quotient rule on this system is a horror, so I won't do it here. Write back if you want to see it.
|
|
|