Question 1180227: True or False, if False provide a counterexample: For functions a & b defined on the entire real line, if both a and b are not bounded on R (Real), then the limit to infinity of the product of a and b cannot exist.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
True or False, if False provide a counterexample:
For functions a & b defined on the entire real line, if both a and b are not bounded on R (Real),
then the limit to infinity of the product of a and b cannot exist.
~~~~~~~~~~~~~~~~~~
F A L S E.
Counter-example:
Let a(x) =  at x =/= 0 and a(0) = 0
(not bounded and not continuous function on R,
but defined over entire R).
Let b(x) = at x =/= 0 and a(0) = 0
(not bounded and not continuous function on R,
but defined over entire R).
Let b(x) = 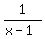 at x =/= 1 and b(1) = 0
(not bounded and not continuous function on R
but defined over entire R).
The limit of a(x)*b(x) at x --> -oo does exist and is equal to 0 (zero).
The limit of a(x)*b(x) at x --> oo does exist and is equal to 0 (zero). at x =/= 1 and b(1) = 0
(not bounded and not continuous function on R
but defined over entire R).
The limit of a(x)*b(x) at x --> -oo does exist and is equal to 0 (zero).
The limit of a(x)*b(x) at x --> oo does exist and is equal to 0 (zero).
Solved, answered and explained.
//////////////
Probably, the answer would be different, had the problem require functions a(x) and b(x) be continuous;
but in the given post, there is NO such a requirement, so I used this fact and constructed counter-example with
discontinuous functions.
|
|
|