Question 1175584: Find the vertex, focus, directrix, and focal width of the parabola. Show the graph.

Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the vertex, focus, directrix, and focal width of the parabola. Show the graph.

 is the standard equation for a right-left facing parabola with vertex at ( is the standard equation for a right-left facing parabola with vertex at ( , , ) )
and a focal length 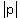
so,
the vertex is at: ( , , ) )
A parabola is the locus of points such that the distance to a point (the focus ) equals the distance to a line (the directrix).
 => => 
Parabola is symmetric around the x-axis and so the directrix is a line parallel to the y-axis, a distance 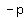 from the center ( from the center ( , , ) x-coordinate ) x-coordinate



the focus lies a distance  from the center ( from the center ( , , ) along the x-axis, and it will be at ) along the x-axis, and it will be at
(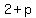 , ,  ) )
(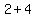 , ,  ) )
( , ,  ) )

|
|
|