Question 1175210: If an even degree polynomial function has a positive leading coefficient, what would a graph like that look like?
Answer by MathLover1(20854)   (Show Source): (Show Source):
You can put this solution on YOUR website!
When you're graphing (or looking at a graph of) polynomials, it can help to already have an idea of what basic polynomial shapes look like. One of the aspects of this is "end behavior", and it's pretty easy. We'll look at some graphs, to find similarities and differences.
First, let's look at some polynomials of even degree with positive and negative leading coefficients:

As you can see above, odd-degree polynomials have ends that head off in opposite directions. If they start "down" (entering the graphing "box" through the "bottom") and go "up" (leaving the graphing "box" through the "top"), they're positive polynomials, just like every positive cubic you've ever graphed. But If they start "up" and go "down", they're negative polynomials.
This behavior is true for all odd-degree polynomials.
simply:
for every polynomial  when when  is is  and and  is is 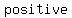 , graph rises to the left and right , graph rises to the left and right
In particular, if the degree of a polynomial  is is  and the leading coefficient is and the leading coefficient is 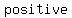 , then , then  → →  as as  → ± → ±  . .
|
|
|