SOLUTION: g={(-6,5),(1,-7),(5,-4),(8,-8)} h(x)=2x+13 Find the following g^-1(5)= h^-1(x)= (h^-1 ∘h)(-8)=

Algebra ->  Rational-functions -> SOLUTION: g={(-6,5),(1,-7),(5,-4),(8,-8)} h(x)=2x+13 Find the following g^-1(5)= h^-1(x)= (h^-1 ∘h)(-8)=      Log On


   

Question 1165631: g={(-6,5),(1,-7),(5,-4),(8,-8)}
h(x)=2x+13
Find the following
g^-1(5)=
h^-1(x)=
(h^-1 ∘h)(-8)=
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
The topic of inverse functions is all about 
interchanging x-coordinates and y-coordinates.

g={(-6,5),(1,-7),(5,-4),(8,-8)}

Find:

g-1(5)=

To find g-1, just swap the coordinates of each point:

g-1 = {(5,-6),(-7,1),(-4,5),(-8,8)}

So g-1(5) = -6

-------------------------------------------

h(x) = 2x+13

Write y for h(x)

y = 2x+13

Interchange x and y

x = 2y+13

Solve for y

x=2y%2B13

2y%2B13=x

2y=x-13

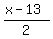%282y%29%2F2+=+%28x-13%29%2F2

y=%28x-13%29%2F2

h-1(x)=%28x-13%29%2F2

-----------------------------------

(h-1∘h)(-8)=

The composition of a function with its inverse or vice-versa
is the identity function y = x, sometimes written I(x) = x.

Therefore, the output is the same as the input.

(h-1∘h)(-8)= I(-8) = -8.

Edwin