|
Question 1157361: Find a rational function with no asymptotes and roots of -3 and 2
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I doubt that the question you ask is what you really intended to ask....
A rational function is a function that is a fraction with polynomials for both numerator and denominator.
(1) To get roots of -3 and 2, we need factors of (x+3) and (x-2) in the numerator. So we can start with

Here is a graph....

That clearly has no asymptotes, and it has roots of -3 and 2.
(2) But that is not enough, because it is not a rational function. We have to have a denominator.
A polynomial in the denominator that has any real zeros will create vertical asymptotes. Since we are not supposed to have any vertical asymptotes, we can't have any polynomial factors in the denominator that have real zeros.
So suppose we make our denominator x^2+1. Our function is now

Here is a graph, along with our original function, showing roots still at -3 an 2....

Oops!!
The graph doesn't show it well; but this function has a horizontal asymptote of y=0.
What happens if we add a linear factor to the numerator to get rid of the horizontal asymptote? Let's try

The new graph, again with the original function, and again showing the roots at -3 and 2....

Well.... That got rid of the horizontal asymptote, but now we have an oblique asymptote.
And if we add a quadratic factor to the numerator instead of another linear factor, we will end up with an asymptote that is a quadratic function.
So by adding a factor in the denominator that has no real roots, we will always get a rational function that still has an asymptote of some kind.
So adding a factor in the denominator that has no real roots will not get us what we need -- a rational function with no asymptotes.
(3) There is one thing left that we can do to our original function, 
We can add linear factors (x-a) (but not (x+3) or (x-2)) to BOTH numerator and denominator. That will give us a function that is equivalent to our original function except at the single point x=a, where there will be a hole in the graph. So that rational function will have roots at -3 and 2 and will have no asymptotes.
So here is a rational function that has roots at -3 and 2 and has no asymptotes. The graph will look exactly the same as our original graph; except there is a hole at (4,14) that you can't see.
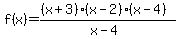
The graphing software on this site won't show the hole in the graph, but a good graphing calculator like my TI-83 will.
CONCLUSION:
To get a rational function with roots at x=-3 and x=2 with no asymptotes, you need
(a) linear factors of (x+3) and (x-2) in the numerator; and
(b) linear factors of (x-a) in both numerator and denominator, where those added linear factors are not (x+3) or (x-2).
|
|
|
| |