SOLUTION: I have a problem that I've done a lot of work on, I think that I have all of the parts but one. Here is the problem: Write a rational function with a hole at the point (1, 3), a ve

Algebra ->  Rational-functions -> SOLUTION: I have a problem that I've done a lot of work on, I think that I have all of the parts but one. Here is the problem: Write a rational function with a hole at the point (1, 3), a ve      Log On


   

Question 1153489: I have a problem that I've done a lot of work on, I think that I have all of the parts but one. Here is the problem: Write a rational function with a hole at the point (1, 3), a vertical asymptote of x = 4, a horizontal asymptote of y = −2, and a double root at (−1, 0).
My work so far:
For VA, x = 4, I put (x-4) in the denominator.
For HA, y = -4, I ensured that ax^n/bx^n = -4, where n is the highest degree of both the numerator and the denominator.
For the double root of (-1,0) I ensured that -b/2a = -1 for the numerator, thus b = 2a.
For the hole at (1,3) I have an issue. I put (x-1) in the numerator and the denominator, but this does not put a hole at the correct place.
My result was (-4x-12)(x-1)/(x-4)(x-1) = (-4x^2-8x+12)/(x^2-5x+4)
I think that this is close but off a bit.
Any help would be fantastic.
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

a rational function with:
a vertical asymptote of x+=+4,
Since f%28x%29 has a vertical is at x+=+4, then the denominator of the rational function contains the term %28x+-+4%29. Function f has the form.
f%28x%29+=+g%28x%29+%2F+%28x+-4+%29

a horizontal asymptote of y+=+-2, then
ax%5En%2Fbx%5En+=a%2Fb=+-2=>a=-2b
a=-2, b=1
f%28x%29+=+-2g%28x%29+%2F+1%28x+-4+%29
a double root at (-1, 0).
g%28x%29 which is in the numerator must be of the same degree as the denominator since f has a horizontal asymptote, and it is y+=+-2 . Also g%28x%29 must contain the term %28x+%2B+1%29 since f has a zero at x+=+-+1.

f%28x%29+=+-2%28x%2B1%29+%2F+%28x+-4+%29
a hole at the point (1, 3), since f%28x%29 has a hole at x+=+1, both the numerator and denominator have a zero at x+=+1 which is term x-1.
f%28x%29+=+-%282%28x%2B1%29%28x-1%29%29+%2F+%28%28x-1%29%28x+-4+%29%29=>your function
expended form:
f%28x%29+=+%28-2x%5E2%2B2%29%2F%28x%5E2-5x%2B4%29

graph:






Answer by greenestamps(13215) About Me  (Show Source):
You can put this solution on YOUR website!


I don't understand what you did for the double root at x=1.

And the solution from the other tutor has a single root at x=1 -- not a double root.

This problem is greatly complicated by requiring a horizontal asymptote at a particular value and a hole in the graph at a particular value.

The requirements are....
(a) a hole at (1,3)
(b) a vertical asymptote at x=4
(c) a horizontal asymptote at y=-2
(d) a double root at x=-1

Note your work shows a horizontal asymptote at y=-4 instead of y=-2. I will assume the y=-2 is the actual requirement.

We'll take care of the vertical asymptote and the double root first -- those are straightforward.

For the vertical asymptote at x=4 we need a factor of (x-4) in the denominator; for a double root at x=-1, we need two factors of (x+1) in the numerator:

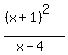
%28%28x%2B1%29%5E2%29%2F%28x-4%29

Next, for the hole at (1,3), we need factors of (x-1) in both numerator and denominator:

%28%28x%2B1%29%5E2%28x-1%29%29%2F%28%28x-4%29%28x-1%29%29

At this point, the degree of the numerator is greater than the degree of the denominator; there will not be a horizontal asymptote. We need an additional factor in the denominator to make the degrees the same.

Furthermore, the additional factor has to be such that the hole in the graph is at (1,3). We need to determine that additional factor.
We first insert a constant factor -2 to get the required horizontal asymptote:

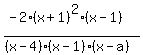
%28-2%28x%2B1%29%5E2%28x-1%29%29%2F%28%28x-4%29%28x-1%29%28x-a%29%29

Now we add the additional unknown factor (x-a) in the denominator and evaluate the function at x=1, ignoring the factors of (x-1) in numerator and denominator, to determine the unknown factor, knowing that the y value at the hole is 3:

%28-2%282%5E2%29%29%2F%28%28-3%29%281-a%29%29+=+3
8%2F%283%281-a%29%29+=+3
8+=+9-9a
9a+=+1
a+=+1%2F9

The required additional factor in the denominator is (x-1/9); the function is now complete:

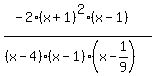
%28-2%28x%2B1%29%5E2%28x-1%29%29%2F%28%28x-4%29%28x-1%29%28x-1%2F9%29%29

A graph with window [-4,4,-2,5] showing the double root at -1:



Note the graphing utility on this forum will not show the hole in the graph; but the graph passes through (1,3).

A graph with window [-40,40,-10,10] showing the horizontal asymptote at y=-2: