Question 1142652: Suppose the functions f, g, h, r and l are defined as follows:
g (x) = sqrt((x − 2)^2) − x/2
Write down Dg and solve the equation g (x) = 0.
Answer by ikleyn(52906)   (Show Source):
You can put this solution on YOUR website! .
For your attention :
THERE ARE NO functions f, h, r, and l in this post.
There is ONLY function g(x), and for it, the solution is as follows.
Solution
The function g(x) is defined as
g(x) =  -  ,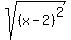
and the equation g(x) = o is
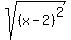- = 0. (1)
The domain is the set of all real numbers.
In this domain, the given equation is equivalent to
= ,
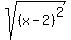which, in turn, is equivalent to
| x - 2 | = . (2)
Vertical lines denote the absolute value.
To solve the equation (2), we consider two cases.
Case 1. x >= 2. In this case
| x - 2 | = x-2; therefore, equation (2) takes the form
x - 2 = .
It is simplified and solved in this way
2x - 4 = x
x = 4.
Case 2. x < 2. In this case
| x - 2 | = -(x-2) = -x + 2; therefore, equation (2) takes the form
-x + 2 = .
It is simplified and solved in this way
-2x + 4 = x
4 = 3x
x = 
ANSWER. The given equation has 2 (two, TWO) solutions : x= 4 and x= .
You can check it on your own by substituting these values of x into the original equation.
Solved, answered, explained, checked and completed.
|
|
|
