Question 1036908: making a round trip from fairview to cartersville, a distance of 20 miles, a pilot faces 30mph head wind one way and 30mph tail wind on the return trip. the return trip takes 45 minutes less than the outbound journey. find the speed of the plane in still air.
Found 4 solutions by josgarithmetic, MathTherapy, ikleyn, Alan3354:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
making a round trip from fairview to cartersville, a distance of 20 miles, a pilot faces 30mph head wind one way and 30mph tail wind on the return trip. the return trip takes 45 minutes less than the outbound journey. find the speed of the plane in still air.
Speed in still air: 
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Making a round trip from Fairview to Cartersville, a distance of 20 miles, a pilot faces 30 mph head wind one way
and 30 mph tail wind on the return trip. The return trip takes 45 minutes less than the outbound journey.
Find the speed of the plane in still air.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "u" be the speed of the plane in still air, in mph.
Then the plane flies at the speed (u+30) mph with the wind, and
at the speed (u-30) against the wind.
The plane spends  = =  hours flying with the wind, and hours flying with the wind, and
 = =  hours flying against the wind.
According to the condition, hours flying against the wind.
According to the condition,  - -  = =  (45 minutes = (45 minutes =  of an hour), which gives an equation of an hour), which gives an equation
 - -  = =  .
Now solve it for u. First multiply both sides by the common denominator 4*(u-30)*(u+30) and then simplify. You will get
80*(u+30) - 80(u-30)= 3(u+30)*(u-30), .
Now solve it for u. First multiply both sides by the common denominator 4*(u-30)*(u+30) and then simplify. You will get
80*(u+30) - 80(u-30)= 3(u+30)*(u-30),
 = = 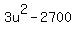 , ,
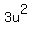 = 4800 + 2700 = 7500, = 4800 + 2700 = 7500,
 = = 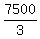 = 2500.
u = = 2500.
u =  = 50 mph (only positive root is acceptable).
Answer. The speed of the plane is 50 mph in still air. = 50 mph (only positive root is acceptable).
Answer. The speed of the plane is 50 mph in still air.
There are other similar solved problems in this site on a plane flying with and against the wind. See the lessons
- Wind and Current problems
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on a plane flying with and against the wind
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|