|
Question 1019514: How would this be solved: 
Thank you
Found 3 solutions by addingup, Edwin McCravy, ikleyn:
Answer by addingup(3677)   (Show Source): (Show Source):
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Answer by ikleyn(52906)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How would this be solved: 
Thank you
------------------------------------------------
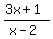 > 2. (1)
1. First, let us assume that x-2 > 0.
In other words, we will look now for solutions in the domain { x | x > 2 }.
Multiply both side of (1) by (x-2), which is positive in this case. Then you will get inequality
3x+1 > 2*(x-2) ---> 3x+1 > 2x-4 ---> 3x - 2x > -4 -1 ---> x > -5.
Thus we obtain this: the solution is the intersection of two sets: {x| x > 2} and {x| x > -5}.
This intersection is the set {x| x > 2}.
So, the interval ( > 2. (1)
1. First, let us assume that x-2 > 0.
In other words, we will look now for solutions in the domain { x | x > 2 }.
Multiply both side of (1) by (x-2), which is positive in this case. Then you will get inequality
3x+1 > 2*(x-2) ---> 3x+1 > 2x-4 ---> 3x - 2x > -4 -1 ---> x > -5.
Thus we obtain this: the solution is the intersection of two sets: {x| x > 2} and {x| x > -5}.
This intersection is the set {x| x > 2}.
So, the interval ( , , ) is the solution to (1), under the assumption that x > 2.
2. Next, let us consider the domain x < 2. In this domain, the denominator (x-2) is negative.
Multiply both side of (1) by (x-2), which is negative now. Then you will get
3x+1 < 2*(x-2). (2)
Notice, that I changed the sign ">" of the original inequality to the opposite sign "<", when
multiplied both sides of (1) by negative number (x-2).
Now, (2) implies 3x+1 < 2x-4 ---> 3x - 2x < -4 -1 ---> x < -5.
Thus by analyzing the domain x < 2 we obtain the solution x < -5.
By collecting the results of n.1 and n.2 you get the full solution set.
It is the union ( ) is the solution to (1), under the assumption that x > 2.
2. Next, let us consider the domain x < 2. In this domain, the denominator (x-2) is negative.
Multiply both side of (1) by (x-2), which is negative now. Then you will get
3x+1 < 2*(x-2). (2)
Notice, that I changed the sign ">" of the original inequality to the opposite sign "<", when
multiplied both sides of (1) by negative number (x-2).
Now, (2) implies 3x+1 < 2x-4 ---> 3x - 2x < -4 -1 ---> x < -5.
Thus by analyzing the domain x < 2 we obtain the solution x < -5.
By collecting the results of n.1 and n.2 you get the full solution set.
It is the union ( , , ) U ( ) U ( , , ).
The problem is solved.
Answer. The solution to (1) is the union ( ).
The problem is solved.
Answer. The solution to (1) is the union ( , , ) U ( ) U ( , , ).
The plot of the function ).
The plot of the function  is shown in Figure. is shown in Figure.
|
 Figure. Plot y =
Figure. Plot y = 
|
|
|
|
| |