|
Question 1209017: A bathroom tub will fill in 15 minutes with both faucets open and the stopper in place. With both faucets closed and the stopper removed, the tub will empty in 20 minutes. How long will it take for the tub to fill if both faucets are open and the stopper is removed?
Found 3 solutions by ikleyn, greenestamps, math_tutor2020:
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A bathroom tub will fill in 15 minutes with both faucets open and the stopper in place.
With both faucets closed and the stopper removed, the tub will empty in 20 minutes.
How long will it take for the tub to fill if both faucets are open and the stopper is removed?
~~~~~~~~~~~~~~~~~~
In this problem, there are two opposite processes.
One process is filling with the rate of 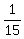 of the volume per minute
(two faucets combined).
Another process is draining with the rate of the volume per minute
(two faucets combined).
Another process is draining with the rate  of the volume per minute.
So, when both facets are open and the stopper is removed, the net filling rate is the difference of the volume per minute.
So, when both facets are open and the stopper is removed, the net filling rate is the difference
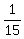 - -  = = 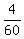 - -  = =  of the volume per minute.
It means that the filling process will take 60 minutes, or 1 hour. ANSWER of the volume per minute.
It means that the filling process will take 60 minutes, or 1 hour. ANSWER
Thus, the problem is just solved (mentally).
If you want to write an equation, you should formalize this reasoning.
Let "t" be the time to fill, in minutes.
Then in t minutes, the two facets will fill  part of the volume,
while through the stopper hole, the part of the volume,
while through the stopper hole, the  part of the volume will be removed.
The volume will be fully filled when part of the volume will be removed.
The volume will be fully filled when
 - -  = 1 (the whole volume).
Write with common denominator and find t = 1 (the whole volume).
Write with common denominator and find t
 - -  = 1, = 1,
 = 1,
t = 60*1 = 60 minutes.
ANSWER. The required time is 60 minutes, or 1 hour. = 1,
t = 60*1 = 60 minutes.
ANSWER. The required time is 60 minutes, or 1 hour.
Solved using equation.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from tutor @ikleyn shows a standard formal algebraic solution and a quick mental solution. While you might require a formal algebraic solution, you should not ignore the fact that solving problems like this mentally is excellent brain exercise.
Here is solution by another method that can be done mentally and quickly. This method can be used to solve many similar "working together" problems.
Consider the least common multiple of the two given times. The two faucets can fill the tub in 15 minutes; the drain can empty the tub in 20 minutes. The least common multiple of those two times is 60 minutes
Now consider what the faucets and drain could accomplish in 60 minutes.
The faucets could fill the tub 60/15 = 4 times; the drain could empty the tub 60/20 = 3 times.
So in 60 minutes with the faucets and drain both operating, the overall result would be filling the tub 4-3 = 1 time.
So the time to fill the tube with both faucets and the drain both operating is 60 minutes, or 1 hour.
ANSWER: 1 hour
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 1 hour
Explanation
Consider a 300 gallon tub.
I arrived at this value by multiplying the given numbers 15 and 20.
There's nothing special about 300 since we can change it to any other value to get the same answer at the end.
If the tub starts off empty, and takes 15 minutes to fill up with stopper in place, then the two faucets have a combined unit rate of 300/15 = 20 gallons per minute.
rate = amountDone/time
After the tub is completely filled up and the faucets turned off, the drain is now opened.
It takes 20 minutes to fully empty.
The drain rate is 300/20 = 15 gallons per minute.
Now consider when both faucets are on and the drain is open at the same time.
In one minute, the faucets add 20 gallons while the drain takes away 15 gallons.
The tub will have 20-15 = 5 gallons.
Meaning that in this tug-of-war of faucets vs drain, the faucets win out to give a net unit rate of 5 gallons per minute.
The tub will ultimately fill up although a bit more slowly of course.
Lets determine how long it takes for the tub to fill up.
rate*time = amountDone
time = amountDone/rate
time = (300 gallons)/(5 gallons per min)
time = (300/5) minutes
time = 60 minutes
time = 1 hour
|
|
|
| |