These problems are like "D=RT" problems, except that the 'distance' is
replaced by 'job to do', The 'job' here is 'one tank'.
An inlet pipe can fill up the tank in 6 hours
So the inlet pipe's filling rate is
while an outlet pipe can empty the tank in 9 hours.
The outlet's emptying rate is considered as a NEGATIVE filling rate.
So the outlet pipe's NEGATIVE filling rate is
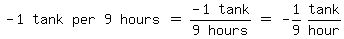
One day, the tank was being filled. When it was 1/3 full, a boy opened the outlet pipe.
So the fraction of a job left to do is to fill 
of a tankful.
How long did it take to fill the rest of the tank?
Now the filling rate is the sum of the rates of the two pipes:
and the job is of a tank.
Just as in "D=RT" problems we use "TIME=DISTANCE/RATE" we use here
"TIME=JOB/RATE". The job is of a tank and the rate is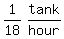 
So,
Edwin
