|
Question 909230: A home builder wants to build a rectangular deck on the back of the house. One side of the deck will share a wall with the house, and the other three sides will have a wooden railing. If the builder has enough wood for 15 meters of railing, what is the area of the largest deck he could build.
Found 2 solutions by Alan3354, ankor@dixie-net.com:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A home builder wants to build a rectangular deck on the back of the house. One side of the deck will share a wall with the house, and the other three sides will have a wooden railing. If the builder has enough wood for 15 meters of railing, what is the area of the largest deck he could build.
-------------
For max area, L = 2W
---
--> W = 5, L = 10
--> 50 sq meters
-------------
I can prove it if necessary.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A home builder wants to build a rectangular deck on the back of the house.
One side of the deck will share a wall with the house, and the other three sides will have a wooden railing.
If the builder has enough wood for 15 meters of railing, what is the area of the largest deck he could build.
:
Since one side is the length of the deck, we can write it
L + 2W = 15
L = (15-2w)
:
Area = L * W
replace L with (15-2w)
A = (15-2w)*W
area is a function of w
f(w) = -2w^2 + 15w
The max area will be when w = the axis of symmetry x = (-b)/(2*a), so we have
w = 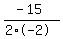
w = 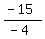
w = +3.75m the width for max area
then
15 - 2(3.75) = 7.5m is the length for max area
:
A = 7.5 * 3.75 = 28.125 sq/m is the max area
|
|
|
| |