SOLUTION: It takes Ralph 5 hours to paint a fence alone. Lisa can do the same job in 10 hours. If Ralph paints alone for 45 minutes before Lisa begins helping, how long must they work togeth

Algebra ->  Rate-of-work-word-problems -> SOLUTION: It takes Ralph 5 hours to paint a fence alone. Lisa can do the same job in 10 hours. If Ralph paints alone for 45 minutes before Lisa begins helping, how long must they work togeth      Log On


   

Question 906517: It takes Ralph 5 hours to paint a fence alone. Lisa can do the same job in 10 hours. If Ralph paints alone for 45 minutes before Lisa begins helping, how long must they work together to finish painting the fence? Give your answer as a simplified fraction.
Found 2 solutions by richwmiller, Edwin McCravy:
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
c/a+ x/a+x/b=1
(45/60)*1/5+ x/5+x/10=1
0.75*1/5+x/5+x/10=1
x/5+x/10=1-0.75/5
x/5+x/10=0.85
x/5+x/10=4.25/5
10x/50+5x/50=42.5/50
15x/50=42.5/50
15x=42.5
x=42.5/15
x=2.83333333 hrs= 2 hr 50 min.
Thanks to Edwin for pointing out my previous silly mistake.




Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
It takes Ralph 5 hours to paint a fence alone. 
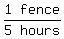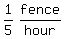
So, Ralph's painting rate is 1 fence per 5 hours or matrix%281%2C2%2C1%2Cfence%29%2Fmatrix%281%2C2%2C5%2Chours%29 or matrix%281%2C2%2C1%2F5%2Cfence%2Fhour%29

Lisa can do the same job in 10 hours. 
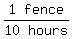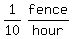
So, Lisa's painting rate is 1 fence per 10 hours or matrix%281%2C2%2C1%2Cfence%29%2Fmatrix%281%2C2%2C10%2Chours%29 or matrix%281%2C2%2C1%2F10%2Cfence%2Fhour%29

If Ralph paints alone for 45 minutes...
That's 3%2F4ths of an hour. so his rate times his time is
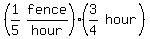
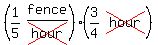
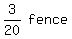%28matrix%281%2C2%2C1%2F5%2Cfence%2Fhour%29%29%2A%28matrix%281%2C2%2C3%2F4%2Chour%29%29%22%22=%22%22%22%22=%22%22matrix%281%2C2%2C3%2F20%2Cfence%29

So Ralph has painted only 3%2F20ths of a fence, and so thete is
1-17%2F20=20%2F20-3%2F20=17%2F20ths of the fence left to paint.

...before Lisa begins helping, 
Now their combined rate then is the sum of their individual rates: matrix%281%2C2%2C1%2F5%2B1%2F10=2%2F10%2B1%2F10=3%2F10%2Cfence%2Fhour%29

how long must they work together to finish painting the fence? 
Let the number of hours be x.  Then during those x hours they
paint the remaining 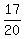17%2F20ths of the fence:
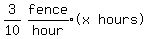
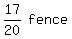
matrix%281%2C2%2C3%2F10%2Cfence%2Fhour%29%2Amatrix%281%2C2%2C%22%28x%22%2C%22hours%29%22%29%22%22=%22%22matrix%281%2C2%2C17%2F20%2Cfence%29 

expr%283%2F10%29x=17%2F20

Multiply both sides by 20

20%2Aexpr%283%2F10%29x=20%2Aexpr%2817%2F20%29

6x=17

x=17%2F6=2%265%2F6hours or 2 hours 50 minutes.

Edwin