SOLUTION: Two pipes can fill a tank in 18 minutes & 27 minutes individually.A third pipe can empty the full tank in 6 minutes.All the three pipes are opened when the tank was 2/3 full.In how

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Two pipes can fill a tank in 18 minutes & 27 minutes individually.A third pipe can empty the full tank in 6 minutes.All the three pipes are opened when the tank was 2/3 full.In how      Log On


   

Question 824909: Two pipes can fill a tank in 18 minutes & 27 minutes individually.A third pipe can empty the full tank in 6 minutes.All the three pipes are opened when the tank was 2/3 full.In how many minute will the tank become empty?
A)11
B)9
Found 3 solutions by josgarithmetic, Edwin McCravy, AnlytcPhil:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
The rate of DRAINING the tank is when all pipes are open, , tanks per minute.

The tank at 2/3 full and having all three pipes open would be drained when m minutes pass: %281%2F54%29%2Am=2%2F3
m=%282%2F3%29%2854%2F1%29
m=18 minutes

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
The above answer is wrong because he goofed in combining the fractions.  He 
used draining rate as positive and filling rate as negative.  The correction of
his method down below the following solution.  But here is my way of working
it with explanation:
Two pipes can fill a tank in 18 minutes & 27 minutes individually.
So the rate of the first pipe is 1 tank per 18 minutes,
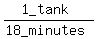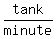or %281_tank%29%2F%2818_minutes%29, or 1%2F18tank%2Fminute

and the rate of the second pipe is 1 tank per 27 minutes,
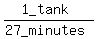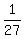
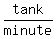or %281_tank%29%2F%2827_minutes%29, or 1%2F27tank%2Fminute.
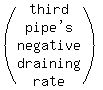
A third pipe can empty the full tank in 6 minutes.
and the rate of the third pipe is the loss of 1 tank or -1 tank per 6 minutes,
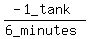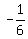
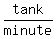or %28-1_tank%29%2F%286_minutes%29, or -1%2F6tank%2Fminute.
All the three pipes are opened when the tank was 2/3 full.
In how many minute will the tank become empty?
Let the answer be x minutes.

Then the combined negative rate of all three pipes is -2%2F3 tank per x minutes,
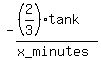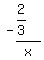
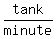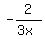
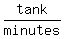or -%28%282%2F3%29tank%29%2F%28x_minutes%29, or -%282%2F3%29%2Fxtank%2Fminute or -2%2F%283x%29tank%2Fminutes.

The equation comes from:

%28matrix%285%2C1%2C%0D%0Afirst%2C%22pipe%27s%22%2Cpositive%2Cfilling%2C+rate%29%29%22%22%2B%22%22%28matrix%285%2C1%2C%0D%0Asecond%2C%22pipe%27s%22%2Cpositive%2Cfilling%2C+rate%29%29%22%22%2B%22%22%28matrix%285%2C1%2C%0D%0Athird%2C%22pipe%27s%22%2Cnegative%2Cdraining%2C+rate%29%29 %22%22=%22%22 %28matrix%285%2C1%2C%0D%0Atheir%2Ccombined%2Cnegative%2Cdraining%2C+rate%29%29

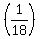
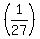
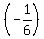
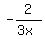
%281%2F18%29%22%22%2B%22%22%281%2F27%29%22%22%2B%22%22%28-1%2F6%29 %22%22=%22%22 -2%2F%283x%29

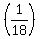
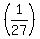
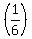
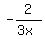%281%2F18%29%22%22%2B%22%22%281%2F27%29%22%22-%22%22%281%2F6%29 %22%22=%22%22 -2%2F%283x%29

Multiply through by LCD = 54x

3x + 2x - 9x = -36
         -4x = -36
           x = 9

Answer = 9 minutes.  

Edwin

Answer by AnlytcPhil(1806) About Me  (Show Source):
You can put this solution on YOUR website!
Here is the correction of the first tutor's method, using draining rate
instead of filling rate:

The rate of DRAINING the tank is when all pipes are open,
, tanks per minute.

The tank at 2/3 full and having all three pipes open would be drained
when m minutes pass: %282%2F27%29%2Am=2%2F3
m=%282%2F3%29%2827%2F2%29
m=9 minutes
Edwin