SOLUTION: 15 workers finish a work in 8 days. How many days would be taken from 12 workers to finish the same work? thank you :)

Algebra ->  Rate-of-work-word-problems -> SOLUTION: 15 workers finish a work in 8 days. How many days would be taken from 12 workers to finish the same work? thank you :)       Log On


   

Question 734386: 15 workers finish a work in 8 days. How many days would be taken from 12 workers to finish the same work? thank you :)
Found 2 solutions by josmiceli, Edwin McCravy:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
15 workers take 8 days to do a job
-----------
1/5 as many workers take 5 times as long to do the job
so, 3 workers take 40 days to do the job
-----------
4 times that many workers can do the job in 1/4 that time, so
12 workers can do the job in 10 days


Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
15 workers finish a work in 8 days. How many days would be taken from 12 workers to finish the same work?
-----------------------------------------------------------------------
Method 1:


The least common multiple of 15 workers and 12 workers is 60 workers.
15 workers is 1/4th of 60 workers and 12 workers is 1/5th of 60 workers.

15 workers finish a work in 8 days. 
So 4 times as many workers can finish the work in 1/4 the time.

So 60 workers can finish it in only 2 days.

So one-fifth as many workers will take 5 times as long, or 10 days.

-----------------

Method 2:

You can also use the worker-time-job formula, which is:

%28W%5B1%5DT%5B1%5D%29%2FJ%5B1%5D%22%22=%22%22%28W%5B2%5DT%5B2%5D%29%2FJ%5B2%5D

where

W1 = the number of workers in the first situation.
T1 = the number of time units (days in this case) in the first situation.
J1 = the number of jobs in the first situation.

W2 = the number of workers in the second situation.
T2 = the number of time units (days in this case) in the second situation.
J2 = the number of jobs in the second situation.

W1 = 15             W2 = 12     
T1 =  8             T2 = the unknown quanity
J1 =  1             J2 = 1

%28W%5B1%5DT%5B1%5D%29%2FJ%5B1%5D%22%22=%22%22%28W%5B2%5DT%5B2%5D%29%2FJ%5B2%5D

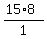
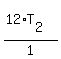%2815%2A8%29%2F1%22%22=%22%22%2812%2AT%5B2%5D%29%2F1

15*8 = 12*T2

 120 = 12*T2

 120%2F12 = T2

  10 = T2 

Answer 10 days.

Edwin