|
Question 732913: PumP A, working alone, can fill a tank in 3 hours, and pump B can fill tthe same tank in 2 hours. If the tank is empty to start and pump a is switched on for 1 hour, after which pump b is also switched on and the two work together, how many minutes will pump b have been working by the time the pool is filled?
Found 2 solutions by lynnlo, ikleyn:
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by ikleyn(53619)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Pump A, working alone, can fill a tank in 3 hours, and pump B can fill the same tank in 2 hours.
If the tank is empty to start and pump A is switched on for 1 hour, after which pump B is also switched on
and the two work together, how many minutes will pump B have been working by the time the pool is filled?
~~~~~~~~~~~~~~~~~~~~~~~~
On the way, the tank was transformed into the pool,
but I will consider this transformation as playing words.
So, we know that pump A fills the tank in 3 hours = 180 minutes, working alone,
while pump B fills the tank in 2 hours = 120 minutes working alone.
When pump A worked alone during 1 hour, it filled 1/3 of the tank volume;
so, 2/3 of the volume remained to fill.
Pump A fills 1/180 of the tank volume per minute;
pump B fills 1/120 of the tank volume per minute.
Working together, two pumps fill
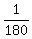 + +  = = 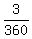 + + 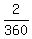 = =  = = 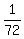 of the tank volume per minute.
And these two pumps should fill 2/3 of the tank volume.
It will take for them
of the tank volume per minute.
And these two pumps should fill 2/3 of the tank volume.
It will take for them
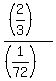 = = 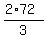 = 2*24 = 48 minutes.
ANSWER. Pump B will work 48 minutes together with pump A to fill the tank. = 2*24 = 48 minutes.
ANSWER. Pump B will work 48 minutes together with pump A to fill the tank.
Thus the problem is just solved completely.
As you see from my post, my solution even does not require using equation:
it only requires manipulating with fractions.
|
|
|
| |