SOLUTION: If Hose A fills a bucket in 45 minutes and Hose B can fill the same bucket in 30 minutes, how long will it take both hoses to fill the same bucket?

Click here to see ALL problems on Rate-of-work-word-problems

Question 725396: If Hose A fills a bucket in 45 minutes and Hose B can fill the same bucket in 30 minutes, how long will it take both hoses to fill the same bucket?
Found 2 solutions by josmiceli, Edwin McCravy:
Answer by josmiceli(19441) (Show Source):
You can put this solution on YOUR website!
Let = minutes to fill bucket with both hoses
Add their rates of filling
( 1 bucket / 45 min ) + ( 1 bucket / 30 min ) = 1 bucket / t min

Multiply both sides by

It takes 18 minutes to fill bucket with both hoses
check:

OK

Answer by Edwin McCravy(20054) (Show Source):
You can put this solution on YOUR website!
If Hose A fills a bucket in 45 minutes and Hose B can fill the same bucket in 30 minutes, how long will it take both hoses to fill the same bucket?
>>...Hose A fills a bucket in 45 minutes...<<

Therefore Hose A's filling rate is 1 bucket per 45 min 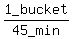or or

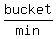
>>...Hose B can fill the same bucket in 30 minutes...<<

Therefore Hose B's filling rate is 1 bucket per 30 min or or

>>...How long will it take both hoses to fill the same bucket?...<<

Let the answer be x minutes. Therefore their combined filling rate is 1 bucket per x min or or . The equation is: Get an LCD of 90x, multiply through and get x = 18 minutes. Edwin