SOLUTION: Working together, Linda and Kathy can clean a beach house in 5.14 hours. Had she done it alone it would have taken Linda 11 hours. How long would it take Kathy to do it alone?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Working together, Linda and Kathy can clean a beach house in 5.14 hours. Had she done it alone it would have taken Linda 11 hours. How long would it take Kathy to do it alone?       Log On


   

Question 686438: Working together, Linda and Kathy can
clean a beach house in 5.14 hours. Had she
done it alone it would have taken Linda 11
hours. How long would it take Kathy to do
it alone?
Working
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
>>Working together, Linda and Kathy can clean a beach house in 5.14 hours.<<
So, their rate working together is 1 house per 5.14 hours or 
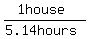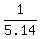
%281house%29%2F%285.14hours%29 or 1%2F5.14house%2Fhours

>>Had she done it alone it would have taken Linda 11 hours.<< 
So, Linda's rate working alone is 1 house per 11 hours or 
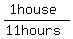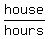
%281house%29%2F%2811hours%29 or 1%2F11house%2Fhours

>>How long would it take Kathy to do it alone?<<
Suppose it would take Kathy x hours to do it alone.

So, Kathy's rate working alone is 1 house per x hours or 
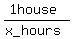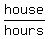%281house%29%2F%28x_hours%29 or 1%2Fxhouse%2Fhours

The equation comes from:

                     


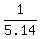                            1%2F11 + 1%2Fx = 1%2F5.14
Eliminate the decimal by multiplying top and bottom of the last fraction
by 100
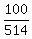                            1%2F11 + 1%2Fx = 100%2F514

Multiply through by 5654x

                       514x + 5654 = 1100x
                              5654 = 586x
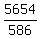                               5654%2F586 = x
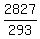                               2827%2F293 = x
                       9.648464164 = x

Round off to hundredths 9.65 hours.

Edwin