|
Question 499228: Mike, Joe and Bill are painting a fence. The painting can be finished if Mike and Joe work together for 4 hours and Bill works alone for 2 hours, or if Mike and Joe work together for 2 hours and Bill works alone for 5 hours, or if Mike works alone for 6 hours, Joe works alone for 2 hours and Bill works alone for 1 hour. How much time does it take each man working alone to complete the painting.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Mike, Joe and Bill are painting a fence.
The painting can be finished if Mike and Joe work together for 4 hours and Bill works alone for 2 hours, or if Mike and Joe work together for 2 hours and Bill works alone for 5 hours, or if Mike works alone for 6 hours, Joe works alone for 2 hours and Bill works alone for 1 hour.
How much time does it take each man working alone to complete the painting.
:
Write an equation for each scenario, let the completed job = 1
:
The painting can be finished if Mike and Joe work together for 4 hours and Bill works alone for 2 hours,"
 + + 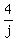 + + 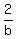 = 1 = 1
:
"if Mike and Joe work together for 2 hours and Bill works alone for 5 hours,"
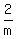 + + 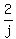 + + 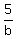 = 1 = 1
:
"if Mike works alone for 6 hours, Joe works alone for 2 hours and Bill works alone for 1 hour."
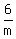 + + 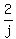 + +  = 1 = 1
:
We are going to use elimination here multiply the 2nd eq by 2, subtract the 1st equation
 + + 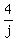 + + 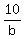 = 2 = 2
 + + 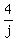 + + 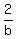 = 1 = 1
---------------------------------------subtraction eliminates m and j, find b
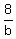 = 1 = 1
b = 8 hrs for Bill alone
:
In the 2nd equation replace b with 8
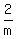 + + 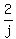 + + 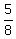 = 1 = 1
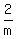 + + 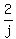 = 1 - = 1 - 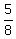
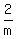 + + 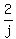 = = 
Do the same with the 3rd equation
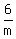 + + 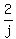 + +  = 1 = 1
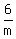 + + 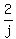 = = 
use these two equation for elimination
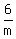 + + 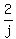 + + 
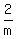 + + 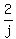 + + 
----------------------------------Subtraction eliminates j, find m
 = = 
m = 8 hrs for Mike alone
:
find j using eq: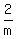 + + 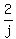 = =  , replace m with 8 , replace m with 8
 + + 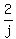 = = 
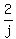 = =  - - 
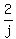 = = 
Cross multiply
j = 2*8
j = 16 hrs for Joe alone
:
to do the job alone: m = 8 hrs, j = 16 hrs, b = 8hrs
:
:
Confirm this in the 1st equation
 + +  + +  = 1 = 1
which is
 + +  + +  = 1 = 1
|
|
|
| |