Question 446848: a new machine can make 10,000 aluminum cans three times faster than an older machine. with both machines working, 10,000 cans be made in 9h. how long would it take the new machine, working alone, to make the 10,000 cans?
Found 4 solutions by mananth, ikleyn, josgarithmetic, MathTherapy:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! older machine x cans /hour
new machine 3x cans /hour
..
both working ---10,000 cans - 9 hours
1 hour 10000/9 = 1111 cans /hour
3x+x= 1111 ( rounded off)
4x=1111
x= 1111/4
x= 277 cans /hour
new machine 3*277 = 831
Answer by ikleyn(53427)  (Show Source):
You can put this solution on YOUR website! .
a new machine can make 10,000 aluminum cans three times faster than an older machine.
with both machines working, 10,000 cans be made in 9h. how long would it take the new machine,
working alone, to make the 10,000 cans?
~~~~~~~~~~~~~~~~~~~~~~
First, I want to say to the writer/(creator of this problem) and to the readers,
that this problem is good, interesting and educative. But it is formulated unprofessionally
in the post. As presented, its meaning is dark, and wording does not correspond to the rules
of using words in English. (Words sound anti-harmonic). So, I will re-formulate it in the right way:
A new machine can make 3 aluminum cans in the same time as an older machine
makes 1 can. With both machines working together, 10,000 cans be made in 9h.
How long would it take the new machine, working alone, to make the 10,000 cans?
With this modified formulation, it is a standard classic entertainment problem,
which can be solved mentally, using reasoning and common sense.
See my solution below.
During this time interval of 9 hours, of 10,000 cans total, 7500 are made by the new machine
and 2500 cans are made by the old machine. (it is because 7500 cans is three times 2500 cans).
So, we need to determine, how much time the new machine needs to produce 2500 cans.
But it is obvious: since the new machine produces 7500 cans in 9 hours, it will produce
one third, or 2500 cans in one third time of 9 hours, i.e. in 3 hours.
Thus, in all, the new machine needs 9 + 3 = 12 hours to produce 10,000 cans working alone.
Solved completely in this modified formulation.
--------------------
After this my solution, you can ignore the post by @mananth,
since it goes out the target.
/\/\/\/\/\/\/\/\/\/\/\/
Keep in mind that the "solution" in the post by @josgarithmetic is incorrect and irrelevant.
The best what you can do regarding the post by @josgarithmetic is to ignore it.
Answer by josgarithmetic(39702)  (Show Source):
Answer by MathTherapy(10587)  (Show Source):
You can put this solution on YOUR website!
a new machine can make 10,000 aluminum cans three times faster than an older machine. with both machines working,
10,000 cans be made in 9h. how long would it take the new machine, working alone, to make the 10,000 cans?
More LIKELY/Chances are, "three times faster......." should actually read,"three times as fast......"
If this is so, then:
Let time new machine takes to complete the job (make 10,000 aluminum cans), be T
Then, time old machine takes to complete the job (make 10,000 aluminum cans), is 3T
In 1 hour then, and working ALONE, new and old machines can do 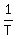 , and  of job, respectively
Since both, working together, can do the job in 9 hours, we then get: 
9 + 3 = T -- Multiplying by LCD, 9T
Time both take, working together, to complete the job (make 10,000 aluminum cans) = 12 hours
|
|
|
