|
Question 400043: Al can complete a particular job in 8 hours. Boris can complete the same
job in 5 hours. Cody can complete a second job, which requires twice as
much work as the first, in 8 hours. If all three people work together on
the larger job for 2 hours, how long, in hours, would it take Al, working
alone, to finish the job?
A 0.8 B 3.0 C 6.8 D 8.0 E 8.8
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Al can complete a particular job in 8 hours.
Boris can complete the same job in 5 hours.
Cody can complete a second job, which requires twice as much work as the first, in 8 hours.
If all three people work together on the larger job for 2 hours, how long,
in hours, would it take Al, working alone, to finish the job?
:
The way I understand it, the larger job, which is twice as much work, would require:
Al = 16 hrs alone
Boris = 10 hrs alone
Cody remains at 8 hrs alone
:
The the completed job = 1
Let t = time required by Cody to finish the job
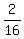 + +  + +  = 1 = 1
Multiply by 80
80*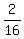 + 80* + 80* + 80* + 80* = 80 = 80
Cancel the denominators and you have
5(2) + 8(2) + 10(t+2) = 80
:
10 + 16 + 10t + 20 = 80
:
10t + 46 = 80
:
10t = 80 - 46
10t = 34
t = 
t = 3.4 hrs for Cody to finish the job
:
I know this is not one of the given answers, but that's what I get.
:
Check this: Cody works 5.4 hrs total
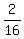 + +  + + 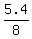
.125 + .200 + .675 = 1; confirms our solution
|
|
|
| |