|
Question 1181303: Carlo can type a manuscript for 10 hours. he started working then bobby joined him 2 hours later. they worked together for 4 hrs until carlo decided to stop and then bobby had to finish the manuscript alone. if bobby finished the remaining portion in 6 more hours, how long can he type the whole manuscript working alone?
Found 5 solutions by mananth, ikleyn, MathTherapy, greenestamps, CPhill:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider typing a manuscript is 1 job
Carlo takes 10 hours to do the job alone
So he does 1/10 of the job in 1 hour
in the first two hours he does 2/10 of the job ------------A
let bobby take x hours to do the job alpne
so he does 1/x of the job in 1 hour
together they do (1/10 +1/x ) of the job in 1 hour
they work together for4 hours.
so they do 4 (1/10 + 1/x ) job = 4(10+x)/10x = 2(10+x)/5x of the job-----B
Booby works for 6 hours
so he does 6/x of the job -------------C
A+B+c = 1 job
2/10 + 2(10+x)/5x + 6/x =1
Solve for x
Answer by ikleyn(53619)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Carlo can type a manuscript for 10 hours. He started working then Bobby joined him 2 hours later.
they worked together for 4 hrs until Carlo decided to stop and then Bobby had to finish the manuscript alone.
if Bobby finished the remaining portion in 6 more hours, how long can he type the whole manuscript working alone?
~~~~~~~~~~~~~~~~~~~~~~~~
To this problem, I will give two solutions: first Arithmetic and the second Algebra.
Arithmetic solution
Carlo's rate of work is 1/10 of the job per hour.
Carlo typed 2 hours + 4 hours = 6 hours and made  + + = =  of the job in 6 hours.
So, the remaining job, which was 1 - of the job in 6 hours.
So, the remaining job, which was 1 -  = =  = =  , was done by Bobby.
Bobby worked 4 hours + 6 hours = 10 hours and completed , was done by Bobby.
Bobby worked 4 hours + 6 hours = 10 hours and completed  of the job.
Hence, Bob's rate of work was of the job.
Hence, Bob's rate of work was 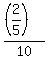 = = 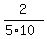 = = 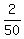 = =  .
It means that Bobby takes 25 hours to print the entire manuscript alone. ANSWER
Algebra solution
Carlo's rate of work is 1/10 of the job per hour.
Let 'b' be the Bobby's rate of work. It is unknown value now, for which we should set uo an equation and find it.
In 2 hours, Carlo made .
It means that Bobby takes 25 hours to print the entire manuscript alone. ANSWER
Algebra solution
Carlo's rate of work is 1/10 of the job per hour.
Let 'b' be the Bobby's rate of work. It is unknown value now, for which we should set uo an equation and find it.
In 2 hours, Carlo made  = =  of the job.
In the next 4 hours, Carlo made of the job.
In the next 4 hours, Carlo made  = =  of the job.
During these 4 hours, Bobby made 4b parts of the job.
In next 6 hours, Bobby completed the job.
So, we write an equation for the whole job by summing these parts of the job.
During these 4 hours, Bobby made 4b parts of the job.
In next 6 hours, Bobby completed the job.
So, we write an equation for the whole job by summing these parts
 + +  + 4b + 6b = 1.
Simplify and find 'b' + 4b + 6b = 1.
Simplify and find 'b'
 + 10b = 1,
10b = 1 - + 10b = 1,
10b = 1 -  = =  ,
b = ,
b = 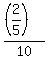 = = 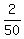 = =  .
Hence, Bobby needs 25 hours to make the whole job working alone.
We get the same answer. .
Hence, Bobby needs 25 hours to make the whole job working alone.
We get the same answer.
Solved in simple manner in two different ways, for your better understanding.
This my solution teaches you on how to solve joint work problems using a conception of the rate of job.
It is MUCH SIMPLER than to follow the @mananth's approach.
Answer by MathTherapy(10719)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Carlo can type a manuscript for 10 hours. he started working then bobby joined him 2 hours later. they worked together for 4 hrs
until carlo decided to stop and then bobby had to finish the manuscript alone. if bobby finished the remaining portion in 6 more
hours, how long can he type the whole manuscript working alone?
Carlo can complete the job in 10 hours, or 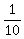 of job in 1 hr
Let time Bobby takes, to do entire job, by himself, be B
Then, Bobby can complete of job in 1 hr
Let time Bobby takes, to do entire job, by himself, be B
Then, Bobby can complete 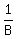 of job in 1 hr
Since Bobby started 2 hours after Carlo, then Carlo worked alone for 2 hours. So, fraction of job completed by Carlo,
before Bobby joined him = of job in 1 hr
Since Bobby started 2 hours after Carlo, then Carlo worked alone for 2 hours. So, fraction of job completed by Carlo,
before Bobby joined him =  With both working together for 4 hrs, fraction of job both completed, working together =
With both working together for 4 hrs, fraction of job both completed, working together = 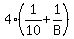 Finally, given that Bobby completed the remaining portion in 6 hours, fraction of entire job done by Bobby, alone, =
Finally, given that Bobby completed the remaining portion in 6 hours, fraction of entire job done by Bobby, alone, = 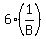 .
We then get the following ENTIRE JOB-equation: .
We then get the following ENTIRE JOB-equation: 

 6B + 100 = 10B ----- Multiplying by LCD, 10B
100 = 10B - 6B
100 = 4B
Time taken by Bobby to do the ENTIRE job, working ALONE, or
6B + 100 = 10B ----- Multiplying by LCD, 10B
100 = 10B - 6B
100 = 4B
Time taken by Bobby to do the ENTIRE job, working ALONE, or 
Answer by greenestamps(13296)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Carlo worked for 2 hours alone and then 4 hours with Bobby, for a total of 6 hours. Since he can do the whole job in 10 hours, the fraction of the job that he did is 6/10 = 3/5.
So Bobby did 2/5 of the job. He worked for 4 hours with Carlo and then 6 more hours alone, for a total of 10 hours.
Since he did 2/5 of the job in 10 hours, the amount of time it would take him to do the job alone is 
ANSWER: 25 hours
Answer by CPhill(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider typing a manuscript is 1 job
Carlo takes 10 hours to do the job alone
So he does 1/10 of the job in 1 hour
in the first two hours he does 2/10 of the job ------------A
let bobby take x hours to do the job alpne
so he does 1/x of the job in 1 hour
together they do (1/10 +1/x ) of the job in 1 hour
they work together for4 hours.
so they do 4 (1/10 + 1/x ) job = 4(10+x)/10x = 2(10+x)/5x of the job-----B
Booby works for 6 hours
so he does 6/x of the job -------------C
A+B+c = 1 job
2/10 + 2(10+x)/5x + 6/x =1
Solve for x
|
|
|
| |