|
Question 1179655: The bird capable of the fastest flying speed is the swift. A swift flying with the wind to a favorite feeding spot traveled 42 mi in 0.3 h. On returning, now against the wind, the swift was able to travel only 27 mi in the same amount of time. What is the rate of the swift in calm air, and what was the rate of the wind?
Found 4 solutions by josgarithmetic, mananth, ikleyn, n2:
Answer by josgarithmetic(39736)   (Show Source): (Show Source):
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! swift speed= x km/h
wind speed= y km/h
with wind speed= (x+y)
against wind speed (x-y)
d= 42 with wind
42 / (x+y) = 0.3
divide by 0.3 0.3
140 / (x+y) = 1
(x+y) = 140 ............1
d= = 27
18/(x-y) = 0.3
divide by 0.3
60 /(x-y) = 1
x - y = 60 .............2
add up (1) & (2)
2 x = 200
/ 2
x= 100 mph speed of swift without wind
plug value of x in (1)
we get y= 40 mph speed of wind
Answer by ikleyn(53619)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The bird capable of the fastest flying speed is the swift. A swift flying with the wind to a favorite feeding spot
traveled 42 mi in 0.3 h. On returning, now against the wind, the swift was able to travel only 27 mi
in the same amount of time. What is the rate of the swift in calm air, and what was the rate of the wind?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution to this problem in the post by @mananth is INCORRECT.
It is incorrect due to arithmetic error in his calculations.
In this my post, I provide short, correct and straightforward solution to the given problem.
Let x be the rate of the swift in calm air, in miles per hour.
Let y be the rate of the wind.
Then the effective speed of the swift with the wind is (x+y) mph,
while the effective speed of the swift against the wind is (x-y) mph,
From the problem, the effective rate of the swift with the wind is the distance divided by the travel time
 = 140 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time = 140 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time
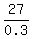 = 90 miles per hour.
So, we have these two equations
x + y = 140 (1)
x - y = 90 (2)
To find x, add the equation. You will get
2x = 140 + 90 = 230, x = 230/2 = 115.
Now express y from equation (1) and calculate
y = 140 - x = 140 - 115 = 25.
At this point the problem is solved completely.
ANSWER. The speed of the swift in calm air is 115 mph. The rate of the wind is 25 mph. = 90 miles per hour.
So, we have these two equations
x + y = 140 (1)
x - y = 90 (2)
To find x, add the equation. You will get
2x = 140 + 90 = 230, x = 230/2 = 115.
Now express y from equation (1) and calculate
y = 140 - x = 140 - 115 = 25.
At this point the problem is solved completely.
ANSWER. The speed of the swift in calm air is 115 mph. The rate of the wind is 25 mph.
Solved correctly.
-------------------------------
The solution by @mananth is defective, since it contains arithmetic errors.
It is also defective methodically, since it contain excessive unnecessary calculations.
We, the tutors, write here our solutions not only to get certain numerical answer.
We write to teach - and, in particular, to teach solving in right style.
This style solving presented in my post, is straightforward with no logical loops.
The solution presented in the post by @mananth has two logical loops.
One loop in the @mananth post is writing
d/r = t ---> 42/(x+y) = 0.3 ---> 0.3x + 0.3y = 42 ---> /0.3 ---> x+y = 42/0.3 = 140,
while in my solution I simply write for the effective rate
u + v = 42/0.3 = 140.
Second loop in the @mananth post is writing
27/(x-y) = 0.3 ---> 0.3x - 0.3y = 27 ---> /4 ---> x-y = 27/0.3 = 60 (error: must be 90),
while in my solution I simply write for the effective rate upstream
u - v = 27/0.3 = 90.
It is why I presented my solution here and why I think it is better than the solution by @mananth:
- because it teaches students to present their arguments in a straightforward way, without logical zigzags.
@mananth repeats his construction of solution with no change for all similar problems on flies
with and against the wind simply because his COMPUTER CODE is written this way.
But this way is not pedagogically optimal - in opposite, it is pedagogically imperfect.
Answer by n2(54)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The bird capable of the fastest flying speed is the swift. A swift flying with the wind to a favorite feeding spot
traveled 42 mi in 0.3 h. On returning, now against the wind, the swift was able to travel only 27 mi
in the same amount of time. What is the rate of the swift in calm air, and what was the rate of the wind?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the rate of the swift in calm air, in miles per hour.
Let y be the rate of the wind.
Then the effective speed of the swift with the wind is (x+y) mph,
while the effective speed of the swift against the wind is (x-y) mph,
From the problem, the effective rate of the swift with the wind is the distance divided by the travel time
 = 140 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time = 140 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time
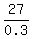 = 90 miles per hour.
So, we have these two equations
x + y = 140 (1)
x - y = 90 (2)
To find x, add the equation. You will get
2x = 140 + 90 = 230, x = 230/2 = 115.
Now express y from equation (1) and calculate
y = 140 - x = 140 - 115 = 25.
At this point the problem is solved completely.
ANSWER. The speed of the swift in calm air is 115 mph. The rate of the wind is 25 mph. = 90 miles per hour.
So, we have these two equations
x + y = 140 (1)
x - y = 90 (2)
To find x, add the equation. You will get
2x = 140 + 90 = 230, x = 230/2 = 115.
Now express y from equation (1) and calculate
y = 140 - x = 140 - 115 = 25.
At this point the problem is solved completely.
ANSWER. The speed of the swift in calm air is 115 mph. The rate of the wind is 25 mph.
Solved correctly.
|
|
|
| |