|
Question 1155509: A and b can paint a wall in 2 hours
A and C can paint the wall in 3 hours
B and C can paint the wall in 4 hours
How long will it take to paint the wall if all 3 work together
Found 3 solutions by josgarithmetic, Alan3354, ikleyn:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let a be the A's rate of work (the part of the job per hour).
Let b ve the B's rate of work;
and let c be the C's rate of work.
We have from the condition
a + b =  (1)
a + c = (1)
a + c =  (2)
b + c = (2)
b + c =  (3)
Add equations (1), (2) and (3) (both sides). You will fet
2a + 2b + 2c = (3)
Add equations (1), (2) and (3) (both sides). You will fet
2a + 2b + 2c =  = =  = =  ;
hence
a + b + c = ;
hence
a + b + c =  . (4)
From equation (4), subtract equation (4). You will get
c = . (4)
From equation (4), subtract equation (4). You will get
c = 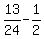 = = 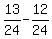 = =  ; hence c = ; hence c =  .
From equation (4), subtract equation (2). You will get
b = .
From equation (4), subtract equation (2). You will get
b = 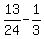 = = 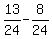 = =  ; hence b = ; hence b =  .
From equation (4), subtract equation (3). You will get
a = .
From equation (4), subtract equation (3). You will get
a = 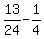 = = 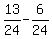 = =  ; hence a = ; hence a =  .
ANSWER. It will take .
ANSWER. It will take 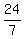 hours for A to complete the job working alone;
It will take hours for A to complete the job working alone;
It will take 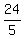 hours for B to complete the job working alone;
It will take hours for B to complete the job working alone;
It will take  hours for C to complete the job working alone. hours for C to complete the job working alone.
Solved.
---------------
It is a classic and canonical way to solve this one and similar other problems for 3 participants.
To see other solved problem by this method, look into the lessons
- Selected joint-work word problems from the archive
- Joint-work problems for 3 participants
in this site.
It is a standard and typical ADVANCED joint work problem.
There is a wide variety of solved joint-work problems with detailed explanations in this site. See the lessons
- Rate of work problems
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Using quadratic equations to solve word problems on joint work
- Solving rate of work problem by reducing to a system of linear equations
- Solving joint work problems by reasoning
- Selected joint-work word problems from the archive
- Joint-work problems for 3 participants
- Had there were more workers, the job would be completed sooner
- One unusual joint work problem
- Special joint work problems that admit and require an alternative solution method
- Joint work word problems for the day of April, 1
- OVERVIEW of lessons on rate-of-work problems
Read them and become an expert in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
/\/\/\/\/\/\/\/\/\/
During several years, I developed and placed these lessons in this site.
During several years I solved joint work problems and touched students and visitors to solve such problems
from introductory level to standard and typical level, and then from typical to advanced level, and then from advanced
to selected and challenging problems.
Not only the visitors learned from my lessons --- the tutors themselves learned a lot from them.
It was and it is a pleasure for me to see the growing interest to solving such problem, and to see the growing level of upcoming problems.
Now I see that the most advanced of these lessons become a subject of interests for visitors.
I am very glad and very proud to see this progress.
|
|
|
| |