|
Question 1150876: Inlet pipes A and B can fill a tank in 6 hours. If the rate of pipe A is twice that of pipe B, find the time of pipe B to fill the tank alone.
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39617)   (Show Source):
Answer by ikleyn(52780)  (Show Source):
You can put this solution on YOUR website! .
Let x be the rate of the pipe B, in the tank volume units per hour.
Then the rate of the pipe A is 2x, according to the condition.
From the condition, you have this equation
6x + 6*(2x) = 1,
saying that both pipes, working together, fill the tank in 6 hours.
From this equation,
6x + 12x = 1
18x = 1
x =  .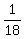
Thus the rate of the pipe B is 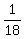of the tank volume per hour.
It means that pipe B will fill the tank in 18 hours, working alone.
Solved.
-------------------
It is a standard and typical joint work problem.
There is a wide variety of similar solved joint-work problems with detailed explanations in this site. See the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Since the rate of pipe A is twice that of pipe B, when the two work together pipe A does 2/3 of the job and pipe B does 1/3 of the job.
It takes the two together 6 hours to fill the tank.
So in those 6 hours that it takes the two pipes together to fill the tank, pipe B fills 1/3 of the tank.
And if pipe B fills 1/3 of the tank in 6 hours, it will take it 18 hours to fill the whole tank alone.
|
|
|
| |
