SOLUTION: The Smith children are responsible for mowing the lawn. If it takes Maria 24 minutes and Bill 40 ​minutes, assuming that they have two lawn​ mowers, how long will it take them

Algebra ->  Rate-of-work-word-problems -> SOLUTION: The Smith children are responsible for mowing the lawn. If it takes Maria 24 minutes and Bill 40 ​minutes, assuming that they have two lawn​ mowers, how long will it take them       Log On


   

Question 1147983: The Smith children are responsible for mowing the lawn. If it takes Maria 24 minutes and Bill 40 ​minutes, assuming that they have two lawn​ mowers, how long will it take them to mow the lawn working​ together?
Found 4 solutions by ikleyn, VFBundy, Alan3354, greenestamps:
Answer by ikleyn(52748) About Me  (Show Source):
You can put this solution on YOUR website!
.

Working alone, Maria makes  1%2F24  of the job per minute.


Working alone, Bill  makes  1%2F40  of the job per minute.


Working together and using two mowers, they make  1%2F24%2B1%2F40 = 5%2F120%2B3%2F120 = 8%2F120 = 1%2F15  of the job per minute.


Hence, it will take  15 minutes  for two persons to complete the job working together.

Solved.

-----------------

It is a standard and typical joint work problem.

There is a wide variety of similar solved joint-work problems with detailed explanations in this site.  See the lessons
    - Using Fractions to solve word problems on joint work
    - Solving more complicated word problems on joint work
    - Selected joint-work word problems from the archive


Read them and get be trained in solving joint-work problems.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems"  of the section  "Word problems".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.


Answer by VFBundy(438) About Me  (Show Source):
You can put this solution on YOUR website!
Rate it takes Maria to mow the lawn working alone = 1/24 lawn per minute
Rate it takes Bill to mow the lawn working alone = 1/40 lawn per minute

Rate it takes both to mow the lawn working together:

1%2F24+%2B+1%2F40 = 5%2F120+%2B+3%2F120 = 8%2F120 = 1/15 lawn per minute

Since they can mow 1/15 of the lawn per minute, it stands to reason it takes them 15 minutes to to mow the entire lawn.

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
24*40/(24+40) = 960/64 = 15 minutes
--------------
Product over sum works for several types of problems.
Parallel flows
Parallel resistors
Parallel work
Maybe some others.
============
Also, the average speed of a round-trip (or 2 legs of equal length) is similar.
If the speeds are R1 and R2, avg = 2*R1*R2/(R1 + R2)

Answer by greenestamps(13195) About Me  (Show Source):
You can put this solution on YOUR website!


If you are taking a timed competitive exam and just want an answer as fast as possible, use the formula shown by tutor @alan. If the individual times for two workers are a and b, then the time working together is 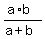%28a%2Ab%29%2F%28a%2Bb%29.

That kind of problem is seen so often that you want to know and use the formula if it is applicable.

But that formula only works for two workers, without any other workers or other complicating factors, such as not having the two workers work for the same amount of time. So you want to know a general algebraic approach that can be used for more complicated problems.

Two other tutors have shown you a solution using the usual algebraic approach.

Here is another algebraic approach that I find many students prefer....

Consider the least common multiple of the times for the two workers. In this problem the times are 24 minutes for Maria and 40 minutes for Bill; the LCM of 24 and 40 is 120.

In 120 minutes, Maria could mow 120/24 = 5 of these lawns; in 120 minutes, Bill could mow 120/40 = 3 of them. So together in 120 minutes they could mow 5+3=8 of the lawns; and that means the amount of time they would take to mow the one lawn is 120/8 = 15 minutes.

The words of explanation make it seem like a long process, but it is not. Without the words, the method looks like this:

LCM(24,40) = 120
120/24 = 5; 120/40 = 3; 5+3=8
120/8 = 15