.
Let me show you three very simple ways to solve this problem.
Solution 1
Let x be the time to fill the tub by the hot water faucet working alone.
Then the time to fill the tub by the cold water faucet working alone is 4x, according to the condition.
It means that when the hot water faucet works alone, it fills  of the tub volume per minute.
It also means that when the cold water faucet works alone, it fills
of the tub volume per minute.
It also means that when the cold water faucet works alone, it fills  of the tub volume per minute.
We also are given, that when two faucets work simultaneously, they fill
of the tub volume per minute.
We also are given, that when two faucets work simultaneously, they fill  of the tube volume per minute.
In other words,
of the tube volume per minute.
In other words,  +
+  =
=  , or
, or
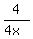 +
+  =
=  ,
,
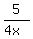 =
=  , hence, 5*3= 4x, or x =
, hence, 5*3= 4x, or x =  minutes =
minutes = 
 minutes = 3 minutes and 45 seconds.
ANSWER. It takes 3 minutes and 45 seconds for hot faucet to fill the bathtub working alone.
minutes = 3 minutes and 45 seconds.
ANSWER. It takes 3 minutes and 45 seconds for hot faucet to fill the bathtub working alone.
Solution 2
Let a be the rate of work of the hot faucet (= which part of the job the hot faucet makes in 1 minute).
Then the rate of work of the cold faucet is 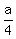 , according to the condition.
Their combined rate of work is the sum of the individual rates, i.e. a +
, according to the condition.
Their combined rate of work is the sum of the individual rates, i.e. a + 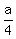 =
= 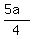 .
It is exactly
.
It is exactly  of the bathtub volume:
of the bathtub volume: 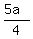 =
=  .
It implies a =
.
It implies a = 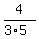 =
= 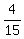 , so the hot faucet fills
, so the hot faucet fills 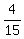 of the tub volume per minute.
It means that it requires
of the tub volume per minute.
It means that it requires  minutes =
minutes = 
 minutes = 3 minutes and 45 seconds to fill the tub.
The same answer.
minutes = 3 minutes and 45 seconds to fill the tub.
The same answer.
Solution 3
Both faucets combined work together as (1+4) = 5 cold faucets simultaneously, and they fill the tube in 3 minutes.
It means that 1 cold faucet will fill the tube in 3*5 = 15 minutes.
One hot faucet will do it in 4 times faster, i.e. in  minutes =
minutes = 
 minutes = 3 minutes and 45 seconds.
The same answer.
minutes = 3 minutes and 45 seconds.
The same answer.
A good student should understand and equally possess (have in his hands and in his mind) all three methods.
---------------
It is a standard and typical joint work problem.
There is a wide variety of similar solved joint-work problems with detailed explanations in this site. See the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.