|
Question 1131263: One roofer can put a new roof on a house three times faster than another. Working together they can roof a house in 5 days. How long would it take the faster roofer working alone?
T/A + T/B = 1
Let T represent their time working together (5 days)
A represents the faster roofer
B represents the other
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39617)   (Show Source):
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
I deleted my first version and re-folmulated my post in this way (as follows):
The solution depends on how you (or me; or another reader) interpret this passage "three times faster".
In English, it is a "dark form", and native English speakers do not use it;
at least, they do not use it when formulate Math problems.
The correct form in English is to say "One roofer's rate of work is 3 times as that of another".
So, I will re-formulate your post in this way:
Working together, two roofers can put a new roof in 5 days. One roofer's rate of work is three times that of another.
How long would it take the faster roofer to complete the job working alone?
Then the solution is as follows.
From the condition, you can write this system of 2 equations in 2 unknowns
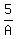 +  = 1 (1)
B = 3A, (2)
where A is the time of the faster roofer and B is the time of the slower roofer.
Substitute (2) into equation (1). You will get
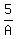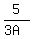+  = 1
Multiply by 3A both sides. You will get
15 + 5 = 3A
3A = 20
A =  hours =   days is the time for the faster roofer.
Time for the slower roofer is 3 times this, i.e. 20 days.
Solved.
-------------------
It is a standard and typical joint work problem.
There is a wide variety of similar solved joint-work problems with detailed explanations in this site. See the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
=================
In your post, you insinuate the problem would be solved algebraically with the use of system of 2 equations.
There is another way of mental solution without using equation/equations.
Under given condition, two roofers are equivalent to 4 slower roofers.
So, we are given that 4 slower roofers can complete the job in 5 days, working together.
It implies immediately, that one single slower roofer can complete the job in 20 = 5*4 days.
Then the time for one faster roofer to do it alone is = days - the same answer.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
NOTE: "3 times faster than..." means 4 times as fast, as indicated in the solution by tutor @ikleyn. The other tutor appears to have worked the problem with the faster working 5 times as fast....
Since the faster worker works 4 times as fast as the slower worker, the faster worker does 4/5 of the work when they are working together. If working together takes them 5 days, then the faster worker does 4/5 of the job in 5 days. So then the time he needs to do the job alone is 5/4 of 5 days: 5*(5/4) = 25/4 days or 6.25 days.
|
|
|
| |
