|
Question 1079936: Please help me solve this word problem thanks!
3 drivers Tom, Zane, and Melissa can deliver all the vehicles from an auction to West coast Shipping warehouse in 12 days. If Zane and Tom work without Melissa, they can deliver all the vehicles in 18 days. If Tom and Melissa work without Zane, they can deliver all the vehicles in 16 days. How many days would it take Melissa to deliver if she works alone.
Answer by ikleyn(52754)   (Show Source):
You can put this solution on YOUR website! .
Please help me solve this word problem thanks!
3 drivers Tom, Zane, and Melissa can deliver all the vehicles from an auction to West coast Shipping warehouse in 12 days.
If Zane and Tom work without Melissa, they can deliver all the vehicles in 18 days.
If Tom and Melissa work without Zane, they can deliver all the vehicles in 16 days.
How many days would it take Melissa to deliver if she works alone.
~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve it for you, but let me first re-formulate the problem.
Tom, Zane and Melissa can do the job in 12 days, working together. (*)
Zane and Tom can do the job in 18 days. (**)
Tom and Melissa can do the job in 16 days. (***)
How many days would it take Melissa to do the job if she works alone.
Solution
Let t be the Tom's rate of work,
z be the Zane's rate of work,
m be the Melissa' rate of work.
Then from the condition
t + z + m =  , (1)
t + z =  , (2)
t + m =  . (3)
Subtract equation (2) from equation (1). You will get
m =  =  =  .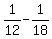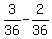
Thus we found that Melissa's rate of work is .
Hence, Melissa can complete the job in 36 days.
Answer. Melissa can complete the job in 36 days working alone.
Solved.
Comments: The equation (3) was not used in the solution.
Hence, the info (***) is excessive and unnecessary in this problem.
The conditions (*) and (**) are enough to get the answer.
There is a wide variety of similar solved joint-work problems with detailed explanations in this site. See the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Using quadratic equations to solve word problems on joint work
- Solving rate of work problem by reducing to a system of linear equations
- Selected joint-work word problems from the archive
- Joint-work problems for 3 participants
in this site.
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Rate of work and joint work problems" of the section "Word problems".
|
|
|
| |
