|
Question 1064533: Find the greatest 4 digit number that has exactly 3 factors.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! That's trial and error.
You do it.
Start with 9999 and count down.
------------
I'm not sure about the other tutor's answer.
1 is not usually considered when factoring.
If 1 is accepted as a factor, then 9409 can be 1*1*1*1*97*97.
And, if 1 is allowed --> 1*17*769 = 9997
If 1 is not allowed ---> 2*19*263 = 9994
=============================================================
---
If using the same factor more than once is allowed, then
then 3*3*11*101 is the solution.
----------------
But, the author of the problem should have specified whether or not to use 1 as a factor.
====================
It's a useless problem, nothing to be learned from it.
9999 9998 9997 9996 9995 9994 9993 9992 9991 9990
2 4999.50 4999.00 4998.50 4998.00 4997.50 4997.00 4996.50 4996.00 4995.50 4995.00
3 3333.00 3332.67 3332.33 3332.00 3331.67 3331.33 3331.00 3330.67 3330.33 3330.00
5 1999.80 1999.60 1999.40 1999.20 1999.00 1998.80 1998.60 1998.40 1998.20 1998.00
7 1428.43 1428.29 1428.14 1428.00 1427.86 1427.71 1427.57 1427.43 1427.29 1427.14
11 909.00 908.91 908.82 908.73 908.64 908.55 908.45 908.36 908.27 908.18
13 769.15 769.08 769.00 768.92 768.85 768.77 768.69 768.62 768.54 768.46
17 588.18 588.12 588.06 588.00 587.94 587.88 587.82 587.76 587.71 587.65
19 526.26 526.21 526.16 526.11 526.05 526.00 525.95 525.89 525.84 525.79
23 434.74 434.70 434.65 434.61 434.57 434.52 434.48 434.43 434.39 434.35
29 344.79 344.76 344.72 344.69 344.66 344.62 344.59 344.55 344.52 344.48
31 322.55 322.52 322.48 322.45 322.42 322.39 322.35 322.32 322.29 322.26
37 270.24 270.22 270.19 270.16 270.14 270.11 270.08 270.05 270.03 270.00
41 243.88 243.85 243.83 243.80 243.78 243.76 243.73 243.71 243.68 243.66
43 232.53 232.51 232.49 232.47 232.44 232.42 232.40 232.37 232.35 232.33
47 212.74 212.72 212.70 212.68 212.66 212.64 212.62 212.60 212.57 212.55
53 188.66 188.64 188.62 188.60 188.58 188.57 188.55 188.53 188.51 188.49
59 169.47 169.46 169.44 169.42 169.41 169.39 169.37 169.36 169.34 169.32
61 163.92 163.90 163.89 163.87 163.85 163.84 163.82 163.80 163.79 163.77
67 149.24 149.22 149.21 149.19 149.18 149.16 149.15 149.13 149.12 149.10
71 140.83 140.82 140.80 140.79 140.77 140.76 140.75 140.73 140.72 140.70
73 136.97 136.96 136.95 136.93 136.92 136.90 136.89 136.88 136.86 136.85
79 126.57 126.56 126.54 126.53 126.52 126.51 126.49 126.48 126.47 126.46
83 120.47 120.46 120.45 120.43 120.42 120.41 120.40 120.39 120.37 120.36
89 112.35 112.34 112.33 112.31 112.30 112.29 112.28 112.27 112.26 112.25
97 103.08 103.07 103.06 103.05 103.04 103.03 103.02 103.01 103.00 102.99
I used Excel, it took just a few minutes.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the greatest 4 digit number that has exactly 3 factors.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If the number has exactly 3 factors, it means that the number is the square of a prime number: N =  .
Then it has the factors 1 (one), p and .
Then it has the factors 1 (one), p and  .
Indeed, if the number is a prime number, it has only TWO factors: 1 (one) and itself.
If the number is not prime and is not the square of a prime, then it has more than 3 factors.
Therefore, to answer the problem's question, we must take the square of the largest two-digit prime number, which is .
Indeed, if the number is a prime number, it has only TWO factors: 1 (one) and itself.
If the number is not prime and is not the square of a prime, then it has more than 3 factors.
Therefore, to answer the problem's question, we must take the square of the largest two-digit prime number, which is 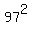 = 9409.
Answer. The number under the question is 9409. = 9409.
Answer. The number under the question is 9409.
Solved.
-------------------
You will spend TOO MUCH your valuable time by checking every number from 9999 down.
So, by giving this solution, I saved a lot of your time.
|
|
|
| |