This Lesson (Introduction to Radicals) was created by by Shruti_Mishra(0)   : View Source, ShowAbout Shruti_Mishra: I am a maths graduate from India and am currently persuing masters in Operations Research.
Radicals are exponents with fractional powers. Alternatively it is inverse of power. For example, 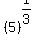 is 5 with fractional power of 1/3. Alternatively this means that the if x = is 5 with fractional power of 1/3. Alternatively this means that the if x = 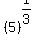 , then , then  . This forms the first property of a radical which we would see in the chapter - Properties of Radicals. A radical is represented using a . This forms the first property of a radical which we would see in the chapter - Properties of Radicals. A radical is represented using a  sign and sign and 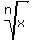 means means 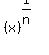 . Radicals are called as roots. Thus . Radicals are called as roots. Thus 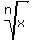 is called as 'n'th root of x. There are special names for n = 2 and 3, which are square root and cube root respectively. is called as 'n'th root of x. There are special names for n = 2 and 3, which are square root and cube root respectively.
Property
If  , then , then  . .
The radicals which cannot be simplified into integers are irrational. When the radical is left completely within the radical sign and not simplified, it is also known as surd. Let us consider a few examples of radicals to understand its usage. We would start with square roots.
Square roots
We know that  and and  . Thus we can inverse these and get the radicals as . Thus we can inverse these and get the radicals as  and and  . Remember that square roots do not need '2' to be put over the radical sign. In these examples, the numbers in the radical are perfect squares and would yield integral answers. However, consider a radical like . Remember that square roots do not need '2' to be put over the radical sign. In these examples, the numbers in the radical are perfect squares and would yield integral answers. However, consider a radical like  , where 2 is not a perfect square. This radical could not be simplified into an integral answer. The value on solving for this would be 1.41421356237 with an infinite decimal sequence. Similarly, for , where 2 is not a perfect square. This radical could not be simplified into an integral answer. The value on solving for this would be 1.41421356237 with an infinite decimal sequence. Similarly, for  the value would be close to 1.73205080756. the value would be close to 1.73205080756.
Cube roots
We know that  and and  . Thus we can inverse these and get the radicals as . Thus we can inverse these and get the radicals as 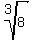 and and 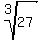 . In these examples, the numbers in the radical are perfect cubes and would yield integral answers. However, consider a radical like . In these examples, the numbers in the radical are perfect cubes and would yield integral answers. However, consider a radical like  , where 5 is not a perfect cube. This radical can not be simplified into an integral answer. The value on solving for this would be close to 1.709975946676 with an infinite decimal sequence. , where 5 is not a perfect cube. This radical can not be simplified into an integral answer. The value on solving for this would be close to 1.709975946676 with an infinite decimal sequence.
Higher roots
For higher roots, we consider exponents such as  and and  . Thus we can inverse these and get the radicals as . Thus we can inverse these and get the radicals as 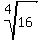 and and 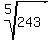 . In these examples, the numbers in the radical are perfect powers and would yield integral answers. However, consider a radical like . In these examples, the numbers in the radical are perfect powers and would yield integral answers. However, consider a radical like 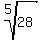 , where 2 is not a perfect square. This radical could not be simplified into an integral answer. The value on solving for this would be close to 1.9472943612303362 with an infinite decimal sequence. , where 2 is not a perfect square. This radical could not be simplified into an integral answer. The value on solving for this would be close to 1.9472943612303362 with an infinite decimal sequence.
Some other examples and values of common radicals
Some common values of radicals are (approximate):





Remember that and radical with 1 would always have value 1, i.e.  for all n. for all n.
Other examples are 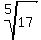 , , 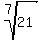 , ,  etc. etc.
This lesson has been accessed 14800 times.
|

 : View Source, Show
: View Source, Show