This Lesson (Solving systems of equations containing radicals) was created by by ikleyn(52778)   : View Source, ShowAbout ikleyn:
Solving systems of equations containing radicals
Problem 1Find x and y if  and and  . .
Solution
Let 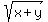 = p. (1)
Then first equation takes the form
p^2 + p - 20 = 0, or, factoring, (p+5)*(p-4) = 0. (2)
Its roots are p= -5 and p= 4.
Due to definition of p (1), we suppose, by default, that "p" is positive; so we choose p= 4.
Hence, x + y = 4^2 = 16. (3)
Let = p. (1)
Then first equation takes the form
p^2 + p - 20 = 0, or, factoring, (p+5)*(p-4) = 0. (2)
Its roots are p= -5 and p= 4.
Due to definition of p (1), we suppose, by default, that "p" is positive; so we choose p= 4.
Hence, x + y = 4^2 = 16. (3)
Let 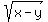 = q. (4)
Then second equation takes the form
q^2 + q - 12 = 0, or, factoring, (q+4)*(q-3) = 0. (5)
Its roots are q= -4 and q= 3.
Due to definition of q (4), we suppose, by default, that "q" is positive; so we choose q= 3.
Hence, x - y = 3^2 = 9. (6)
Thus we have these two equations
x + y = 16 (3)
x - y = 9 (6)
Solving by elimination, we get x = = q. (4)
Then second equation takes the form
q^2 + q - 12 = 0, or, factoring, (q+4)*(q-3) = 0. (5)
Its roots are q= -4 and q= 3.
Due to definition of q (4), we suppose, by default, that "q" is positive; so we choose q= 3.
Hence, x - y = 3^2 = 9. (6)
Thus we have these two equations
x + y = 16 (3)
x - y = 9 (6)
Solving by elimination, we get x = 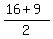 = = 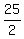 = 12.5; y = 16-x = 16-12.5 = 3.5.
ANSWER. x = 12.5, y = 3.5. = 12.5; y = 16-x = 16-12.5 = 3.5.
ANSWER. x = 12.5, y = 3.5.
My other lessons on solving equations containing radicals are
- HOW TO solve equations containing radicals
- Advanced problems on solving equations containing radicals
- OVERVIEW of my lessons on solving equations containing radicals
in this site.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 664 times.
|

