Tutors Answer Your Questions about Radicals (FREE)
Question 983749: I am currently working on a summer homework packet for my Pre-Calculus class and there is a problem I have come across that I have completely forgotten how to solve. I have tried looking for example problems similar to it but to no avail. I have a picture of it written out and I would appreciate any help I could get on it. Thanks!
http://i.imgur.com/H0xgT5y.jpg
Click here to see answer by MathLover1(20849)   |
Question 987774: how to solve and simplify root 6 times the 6 root of 32
I have tried to simplify inside the roots first and got a hole number of 2 but figure out how to get the radical number.
we are provided the answer of 2 6 root of 108 but I don't understand how to get it step by step.
Click here to see answer by ikleyn(52776)  |
Question 987920: Please help me solve this equation:  I believe I figured out the top part of the equation... 3(^3sqrt54) = 9 (^3sqrt2) but I'm not sure how to handle the bottom part of the equation ^3sqrt18? I believe the final solution is 3(^3sqrt3) just not sure how to get rid of the sqrt/radical in the denominator. Thanks in advance for your help!
Click here to see answer by solver91311(24713)  |
Question 988089: can you help me simplify this radical expression?
the problem is cube root of 16x^4y, minus 3x times the cube root of 2xy, plus 5 times the cube root of -2xy^4
so far i have gotten 2 times the cube root of 2, times the cube root of x^4y, minus 3x times the cube root of 2 times the cube root of xy, plus 5 times times the negative cube root of 2 times the cube root of xy^4
Click here to see answer by Boreal(15235)  |
Question 988089: can you help me simplify this radical expression?
the problem is cube root of 16x^4y, minus 3x times the cube root of 2xy, plus 5 times the cube root of -2xy^4
so far i have gotten 2 times the cube root of 2, times the cube root of x^4y, minus 3x times the cube root of 2 times the cube root of xy, plus 5 times times the negative cube root of 2 times the cube root of xy^4
Click here to see answer by solver91311(24713) |
Question 988368: I am trying to solve this problem but my answer is not the answer in the book. Can you help me figure it out? Here is the equation:
x/(x-3) + 4/(x+5)=8x/((x-3)(x+5))
I have a solution set of{-4,3} but the answer key shows the answer as {4}
Click here to see answer by macston(5194)  |
Question 989465: This is actually a Calculus 1 problem, but I am having problems with the algebra portion. So far, I have determined that I need to multiply this problem by the conjugate of BOTH the numerator and denominator, but I've never done that. Once I get the fraction all worked out and cleaned up, I know how to handle the limit portion.
Evaluate the limit of:
(((6-x)^(1/2))-2) / (((3-x)^(1/2))-1)
as x approaches 2
Here is my work:
(((6-x)^(1/2))-2)/(((3-x)^(1/2))-1) * (((6-x)^(1/2))-2)/(((6-x)^(1/2))-2)
=> (((6-x)^2)-((4)^2))/(((6-x)^(1/2))-2)/(((3-x)^(1/2))-1)
Then do I multiply out the top, and then multiply by the conjugate of the numerator?
=> ((-x^2)-12x+36)/(((6-x)^(1/2))-2)/(((3-x)^(1/2))-1) * (((3-x)^(1/2))-1)/(((3-x)^(1/2))-1)
This is where I'm really confused. How do I multiply a polynomial by the conjugate? Would the numerator be ((-x^2)(3-(x^(1/2)))-12x((3-(x^(1/2))+36((3-x)^(1/2))-x^2+12x-36?
Now what? I appreciate any and all help. Please let me know where I went wrong, and what I need to do to work out the problem.
Click here to see answer by solver91311(24713) |
Question 990388: Can you help me with this? Here is the problem: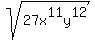
I am trying to symplify this radical equation but i'm stuck. Now the answer key shows the answer as 3x^5y^6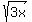
I get where x^5 and y^6 come from but how do they come up with 3 outside and 3x inside. I hope this email makes sense.
Click here to see answer by solver91311(24713) |
Question 990388: Can you help me with this? Here is the problem: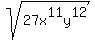
I am trying to symplify this radical equation but i'm stuck. Now the answer key shows the answer as 3x^5y^6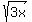
I get where x^5 and y^6 come from but how do they come up with 3 outside and 3x inside. I hope this email makes sense.
Click here to see answer by josmiceli(19441)  |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710
|
