Question 916040: Please help me solve this equation: sqrt(2x+3)-sqrt(x+1)=1
Thank you
Answer by josh_jordan(263)   (Show Source):
You can put this solution on YOUR website! 
1. Isolate one of the square roots by subtracting the other from both sides. In this case, I will add 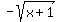 from both sides, giving us
2. Square both sides so that we eliminate the root on the left side. This will give us
3. Combine like terms on the right side, giving us
4. Subtract the 2 on the right side from both sides of the equal sign, which gives us
 ----->
5. Subtract the x on the right side from both sides of the equal sign, which gives us
 ----->
6. Divide both sides of the equation by 2, giving us
7. Square both sides of the equal sign to eliminate the radical on the right side, giving us
8. Multiply both sides of the equal sign by 4 to get rid of the fraction on the left side, giving us:
9. Place all terms on the left side of the equation and set the equation equal to zero:
 ----->
10. Factor the left side of the equation, which will give us
11. Set each factor equal to 0 and solve for x for both factors:
 and -----> and 
12. Verify that both of these values of x work, by plugging them into the original equation and making sure when plugged in, they equal 1.
Final Answer: x = -1 , 3
|
|
|
