SOLUTION: Can you please help me with these questions? a) sq. rt. of 12 plus sq.rt. of 108 b) ^3 sq. rt. of 16 times ^3 sq. rt. of 3 Thank you so much for your help.

Algebra ->  Algebra  -> Radicals -> SOLUTION: Can you please help me with these questions? a) sq. rt. of 12 plus sq.rt. of 108 b) ^3 sq. rt. of 16 times ^3 sq. rt. of 3 Thank you so much for your help.      Log On

Ad: Algebrator™ solves your algebra problems and provides step-by-step explanations!
Ad: Algebra Solved!™: algebra software solves algebra homework problems with step-by-step help!

   

Question 86391: Can you please help me with these questions?
a) sq. rt. of 12 plus sq.rt. of 108
b) ^3 sq. rt. of 16 times ^3 sq. rt. of 3
Thank you so much for your help.
Answer by jim_thompson5910(21667) About Me  (Show Source):
You can put this solution on YOUR website!
a)

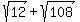
sqrt%2812%29%2Bsqrt%28108%29

First lets simplify sqrt%2812%29:


sqrt%2812%29 Start with the given expression
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. This way the perfect square will become a rational number.
So let's list the factors of 12
Factors:
1, 2, 3, 4, 6,


Notice how 4 is the largest perfect square, so lets break 12 down into 4*3


sqrt%284%2A3%29 Factor 12 into 4*3

sqrt%284%29%2Asqrt%283%29 Break up the square roots using the identity sqrt%28x%2Ay%29=sqrt%28x%29%2Asqrt%28y%29

2%2Asqrt%283%29 Take the square root of the perfect square 4 to get 2

So the expression

sqrt%2812%29

simplifies to

2%2Asqrt%283%29
---------------------------------------------------------------------------
Now lets simplify sqrt%28108%29:


sqrt%28108%29 Start with the given expression
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. This way the perfect square will become a rational number.
So let's list the factors of 108
Factors:
1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54,


Notice how 36 is the largest perfect square, so lets break 108 down into 36*3


sqrt%2836%2A3%29 Factor 108 into 36*3

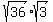sqrt%2836%29%2Asqrt%283%29 Break up the square roots using the identity sqrt%28x%2Ay%29=sqrt%28x%29%2Asqrt%28y%29

6%2Asqrt%283%29 Take the square root of the perfect square 36 to get 6

So the expression

sqrt%28108%29

simplifies to

6%2Asqrt%283%29


So the expression

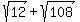
sqrt%2812%29%2Bsqrt%28108%29

simplifies to

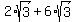
2%2Asqrt%283%29%2B6%2Asqrt%283%29


Notice we have a common term of sqrt%283%29. If we let y=sqrt%283%29 we get

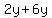
2y%2B6y

Now combine like terms

8y}

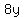Replace y with sqrt%283%29

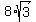
8%2Asqrt%283%29


Check:

Evaluate the given expression with a calculator:

sqrt%2812%29%2Bsqrt%28108%29=13.856406460551

Evaluate the simplified expression with a calculator:

8%2Asqrt%283%29=13.856406460551

Since they are equal (to a certain decimal place), this verifies our answer



================================================================================

b)

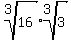
root%283%2C16%29%2Aroot%283%2C3%29

Since the 2 radicands are under the same root value, we can combine them using the identity root%28n%2Cx%29%2Aroot%28n%2Cy%29=root%28n%2Cx%2Ay%29

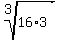root%283%2C16%2A3%29 Combine the cube roots

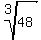root%283%2C48%29 Multiply

root%283%2C8%2A6%29 Factor 48 into 8*6. I chose to factor out an 8 since 8 is a perfect cube

root%283%2C8%29%2Aroot%283%2C6%29 Break up the roots using root%28n%2Cx%2Ay%29=root%28n%2Cx%29%2Aroot%28n%2Cy%29

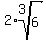2%2Aroot%283%2C6%29 Take the cube root of 8

Check:

Evaluate the given expression with a calculator:

root%283%2C16%29%2Aroot%283%2C3%29=3.63424118566428

Evaluate the simplified expression with a calculator:

2%2Aroot%283%2C6%29=3.63424118566428

Since they are equal (to a certain decimal place), this verifies our answer