SOLUTION: Solve a) √(2x+1) + √(x+1) = 3 Thanks so much in advance:)

Algebra ->  Radicals -> SOLUTION: Solve a) √(2x+1) + √(x+1) = 3 Thanks so much in advance:)      Log On


   

Question 818339: Solve
a) √(2x+1) + √(x+1) = 3
Thanks so much in advance:)
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
sqrt%282x%2B1%29+%2B++sqrt%28x%2B1%29+=+3
Here's a procedure for solving these types of equations (where the variable is inside a radical):
  1. Isolate a radical.
  2. Raise each side of the equation to a power that matches the type of the isolated radical. (This should eliminate the isolated radical but it may not eliminate radicals on the other side.)
  3. If there are still any radicals, repeat steps 1 and 2.
  4. At this point there should no longer be any radicals in the equation. Solve the equation.
  5. If at any point both sides of the equation were raised to an even power, check the solution. (A check may be done if only odd powers were used but it would be optional.)
Let's see this in action:
1. Isolate.
Subtracting the second square root from each side will isolate the first square root:
sqrt%282x%2B1%29+=+-sqrt%28x%2B1%29+%2B+3

2. Since the isolated radical is a square root, square both sides:
%28sqrt%282x%2B1%29%29%5E2+=+%28-sqrt%28x%2B1%29+%2B+3%29%5E2
Squaring the left side is easy. On the right side we must use FOIL or the %28a%2Bb%29%5E2+=+a%5E2%2B2ab%2Bb%5E2 pattern to square it correctly. I prefer using the pattern:
2x%2B1+=+%28-sqrt%28x%2B1%29%29%5E2+%2B+2%28-sqrt%28x%2B1%29%29%283%29+%2B+%283%29%5E2
2x%2B1+=+x%2B1+%2B+%28-6sqrt%28x%2B1%29%29+%2B+9
2x%2B1+=+x%2B10+%2B+%28-6sqrt%28x%2B1%29%29+

3. There is still a radical. So back to step 1.

1. Isolate.
Subtracting x and 10 from each side:
x-9+=+-6sqrt%28x%2B1%29+
The radical on the right is sufficiently isolated. But if that -6 bothers you, you can divide both sides by it.

2. Again we have an isolated square root so we square each side:
%28x-9%29%5E2+=+%28-6sqrt%28x%2B1%29%29%5E2+
To square the left side I will use another pattern: %28a-b%29%5E2+=+a%5E2-2ab%2Bb%5E2
%28x%29%5E2-2%28x%29%289%29%2B+%289%29%5E2+=+%28-6%29%5E2+%2Asqrt%28x%2B1%29%29%5E2
x%5E2-18x%2B+81+=+36%28x%2B1%29+
x%5E2-18x%2B+81+=+36x%2B36+
3. The radicals are all gone. So on to step 4.

4. Solve.
This is a quadratic equation so we want one side to be zero. Subtracting 36x and 36 from each side:
x%5E2-54x%2B+45+=+0
This does not factor. So we will use the quadratic formula:
x+=+%28-%28-54%29%2B-sqrt%28%28-54%29%5E2-4%281%29%2845%29%29%29%2F2%281%29
Simplifying...
x+=+%2854%2B-sqrt%282916-4%281%29%2845%29%29%29%2F2
x+=+%2854%2B-sqrt%282916-180%29%29%2F2
x+=+%2854%2B-sqrt%282736%29%29%2F2
x+=+%2854%2B-sqrt%284%2A684%29%29%2F2
x+=+%2854%2B-sqrt%284%2A4%2A171%29%29%2F2
x+=+%2854%2B-sqrt%284%2A4%2A9%2A19%29%29%2F2
x+=+%2854%2B-sqrt%284%29%2Asqrt%284%29%2Asqrt%289%29%2Asqrt%2819%29%29%2F2
x+=+%2854%2B-+2%2A2%2A3%2Asqrt%2819%29%29%2F2
x+=+%282%2827+%2B-+2%2A3%2Asqrt%2819%29%29%29%2F2
The factors of 2 cancel:
x+=+27+%2B-+2%2A3%2Asqrt%2819%29
x+=+27+%2B-+6sqrt%2819%29
which is short for:
x+=+27%2B6sqrt%2819%29 or x+=+27-6sqrt%2819%29

5. Check.
We did raise the equation to an even power (twice!). So a check is not optional. Use the original equation to check:
sqrt%282x%2B1%29+%2B++sqrt%28x%2B1%29+=+3
Checking x+=+27%2B6sqrt%2819%29:
sqrt%282%2827%2B6sqrt%2819%29%29%2B1%29+%2B++sqrt%28%2827%2B6sqrt%2819%29%29%2B1%29+=+3
Simplifying...
sqrt%2854%2B12sqrt%2819%29%2B1%29+%2B++sqrt%2828%2B6sqrt%2819%29%29+=+3
sqrt%2855%2B12sqrt%2819%29%29+%2B++sqrt%2828%2B6sqrt%2819%29%29+=+3
At this point, with a little thought, we can see that there is a problem. First note that the all the square roots are references to positive square roots. Now look at the first square root:
  • The square root of 55 is between 7 and 8.
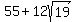  • 55%2B12sqrt%2819%29 will be more than 55.
  • So sqrt%2855%2B12sqrt%2819%29%29 will be even larger than 7.
  • But how can we add number which is larger than 7 to another positive number, 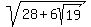sqrt%2828%2B6sqrt%2819%29%29 and end up with 3?
  • Answer: We can't. So the "solution" does not check out! Discard it.

Checking x+=+27-6sqrt%2819%29:
sqrt%282%2827-6sqrt%2819%29%29%2B1%29+%2B++sqrt%28%2827-6sqrt%2819%29%29%2B1%29+=+3
Simplifying...
sqrt%2854-12sqrt%2819%29%2B1%29+%2B++sqrt%2828-6sqrt%2819%29%29+=+3
sqrt%2855-12sqrt%2819%29%29+%2B++sqrt%2828-6sqrt%2819%29%29+=+3
This time we cannot rule out that this solution will check. The best way to finish is to:
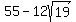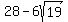  1. Use your calculator to make sure that both 55-12sqrt%2819%29 and 28-6sqrt%2819%29 are positive. If not, then this solution does not check out and therefore, since we've already rejected the only other solution we found, there are no solutions to the equation. If these are both positive, then...
  2. Follow the initial procedure to eliminate the radicals.
  3. Then, if the left side equals the right side, the answer checks out. If not, then there are no solutions.
Since eliminating the radicals would take a long time, I am going to "cheat" and use a less ideal way to finish the check, use my calculator to turn all the square roots into decimal approximations. (I'll be rounding to 4 places.)
sqrt%2855-12%284.3589%29%29+%2B++sqrt%2828-6%284.3589%29%29+=+3
sqrt%2855-52.3068%29+%2B++sqrt%2828-26.1534%29+=+3
sqrt%282.6932%29+%2B++sqrt%281.8466%29+=+3
sqrt%282.6932%29+%2B++sqrt%281.8466%29+=+3
1.6411+%2B+1.3589+=+3
3+=+3 Check!
The reason this way is less ideal than eliminating the square roots is that, because of the rounding, the left side might have turned out to be something like 2.9998 or 3.0001 instead of exactly 3. Then we would not know if the small difference between the left side and the right side is proof that the solution does not work or if it is due to the rounding. Even when the left side and right side are exactly equal, like above, we still do not know for sure that this is proof that the solution checks out!? Maybe, if we used more decimal places, the left side is actually 3.00000003 and not exactly 3!!

Bottom line: The only solution to your equation is x+=+27-6sqrt%2819%29 (we hope!?)