SOLUTION: I need help. :( F(x)= 4 times the square root of (-X^2-25)-10 Solve for f(x)=0

Algebra ->  Radicals -> SOLUTION: I need help. :( F(x)= 4 times the square root of (-X^2-25)-10 Solve for f(x)=0       Log On


   

Question 817589: I need help. :(
F(x)= 4 times the square root of (-X^2-25)-10
Solve for f(x)=0
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Note: For an extremely fast solution, check the P.S. at the end.

f%28x%29=+4%2Asqrt%28-x%5E2-25%29-10
Replace f(x) with 0:
0+=+4%2Asqrt%28-x%5E2-25%29-10
To solve an equation with the variable inside a radical:
  1. Isolate the radical.
  2. Raise each side of the equation to a power to match the type of root. (Square square roots, cube cube roots, raise 4th roots to the 4th power, etc.) (Note: This should eliminate the isolated radical. But if the other side of the equation has a radical, that one might not get eliminated.)
  3. If there are still radicals, repeat steps 1 and 2.
  4. At this point the radicals should be gone. Use techniques appropriate for the type of equation to solve.
  5. If at any point both sides of the equation have been raised to an even power, check your solution(s)!
Let's see this on our equation:
0+=+4%2Asqrt%28-x%5E2-25%29-10
1. Isolate a radical.
Add 10:
10+=+4%2Asqrt%28-x%5E2-25%29
The radical is sufficiently isolated. But if that 4 bothers you, you can divide both sides by 4.

2. Raise to a power.
Since our isolated radical is a square root we will square each side:
%2810%29%5E2+=+%284%2Asqrt%28-x%5E2-25%29%29%5E2
which simplifies as follows...
100+=+16%2A%28-x%5E2-25%29
100+=+-16x%5E2-400

3. Any radicals left?
No. So on to step 4.

4. Solve.
Our equation is now a quadratic equation. We can
  • Make on side a zero and...
    • Try to factor.
      Or...
    • Use the Quadratic formula.

    Or...
  • Isolate the x%5E2 and use a square root.

I am going to use a square root. Adding 400 to each side:
500+=+-16x%5E2
Dividing by -16:
500%2F%28-16%29=x%5E2
At this point we might notice a problem. We have x%5E2 equal to a negative number. This is not possible if x is a real number. So there are no real solutions to this equation.

If you want complex number solutions, read on...
500%2F%28-16%29=x%5E2
Canceling a factor 0f -4 the fraction reduces to:
%28-125%29%2F4=x%5E2
Square root of each side:
0%2B-sqrt%28%28-125%29%2F4%29=sqrt%28x%5E2%29
Simplifying...
+sqrt%28-125%29%2Fsqrt%284%29=x
+sqrt%28-1%2A125%29%2F2=x
+%28sqrt%28-1%29%2Asqrt%28125%29%29%2F2=x
+%28i%2Asqrt%2825%2A5%29%29%2F2=x
+%28i%2Asqrt%2825%29%2Asqrt%285%29%29%2F2=x
+%28i%2A5%2Asqrt%285%29%29%2F2=x
+%285i%2Asqrt%285%29%29%2F2=x
which is short for:
%285i%2Asqrt%285%29%29%2F2=x or -%285i%2Asqrt%285%29%29%2F2=x
In standard a + bi form these would be:
0+%2B+%28%285sqrt%285%29%29%2F2%29i=x or 0+%2B+%28%28-5sqrt%285%29%29%2F2%29i=x

5. Check.
Remember, there are no real solutions to the equation. So if these are the only solutions you want then there is no check to be made. But we did square both sides so if you do want complex solutions we must check. I'll it up to you to check. (They both should work.)

P.S. If you are only interested in real solutions, then look at the radicand ("radicand" is the name for the expression inside a radical) of the function, 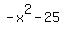-x%5E2-25. You might notice some important things:
  • x%5E2 will either be positive or zero.
  • If x%5E2 is positive or zero, then -x%5E2 will be negative or zero.
  • If we subtract 25 from a negative number or zero, then we end up with a negative number.
  • But a radicand of a real-valued function can never be negative.
  • So there are no values for x that will result in a real value, like 0 for f(x)!!
  • So from just this logic we can know that there are no real numbers for which f(x) = 0.