SOLUTION: help me please i am able to do + but not - sqrt{{{x-1}}}=x-3

Algebra ->  Radicals -> SOLUTION: help me please i am able to do + but not - sqrt{{{x-1}}}=x-3      Log On


   

Question 79040: help me please i am able to do + but not -
sqrtx-1=x-3
Found 2 solutions by jim_thompson5910, stanbon:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
sqrt%28x-1%29=x-3

%28sqrt%28x-1%29%29%5E2=%28x-3%29%5E2 Square both sides

x-1=%28x-3%29%5E2

x-1=x%5E2-6x%2B9 Foil the right side

0=x%5E2-7x%2B10 Get all terms to one side
Use the quadratic formula to solve for x
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-7x%2B10+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-7%29%5E2-4%2A1%2A10=9.

Discriminant d=9 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--7%2B-sqrt%28+9+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-7%29%2Bsqrt%28+9+%29%29%2F2%5C1+=+5
x%5B2%5D+=+%28-%28-7%29-sqrt%28+9+%29%29%2F2%5C1+=+2

Quadratic expression 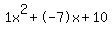1x%5E2%2B-7x%2B10 can be factored:
1x%5E2%2B-7x%2B10+=+1%28x-5%29%2A%28x-2%29
Again, the answer is: 5, 2. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-7%2Ax%2B10+%29


So we get 2 possible solutions:
x=2, x=5
However, we need to check whether or not they work
Plug in x=2
sqrt%282-1%29=2-3
sqrt%281%29=-1
1=-1 Since this is not true, we must discard this possible solution
Plug in x=5
sqrt%285-1%29=5-3
sqrt%284%29=2
2=-2 Since this answer works, this is the only solution
So our answer is
x=5
Notice the 2 graphs only intersect at one spot, which is (5,2)
+graph%28+300%2C+200%2C+-2%2C+10%2C+-10%2C+10%2C+x-3%2C+sqrt%28x-1%29%29+

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
sqrtx-1=x-3
Square both sides to get:
x-1=(x-3)^2
x-1=x^2-6x+9
x^2-7x+10=0
Factor to get:
(x-5)(x-2)=0
x=5 or x=2
-------------------------
Cheers,
Stan H.